Numerous problems in Computer Vision can be reduced to fitting a generic model onto observed data or measurements. An example is identifying 2D shapes (e.g. lines, circles) in an image, where the model is a geometrical structure defined by a few parameters (e.g. slope and intercept, center and radius), and fitting the model onto the data is equivalent to determining the size and position of instances of the shapes in the image. The figure below illustrates.
Computer Vision problems also deal with more exotic models such as subspaces, homographies and fundamental matrices. These models partake in a wide range of applications such as 3D reconstruction from multi-view images and segmentation of moving objects in a dynamic scene.
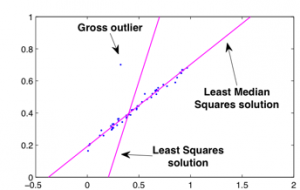
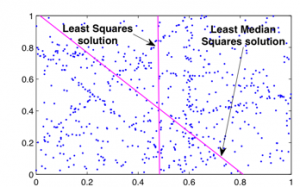
Computer Vision applications constantly deal with very complex data, often automatically captured in unconstrained environments. Outliers are inevitably present in the data due to imperfections in sensing, digitisation and preprocessing. Another feature of data in Computer Vision is the existence of multiple model instances (e.g. multiple motion subspaces, planar homographies). Therefore traditional robust regression methods are simply inadequate for Computer Vision. See figure below.
Surmounting the challenges described above is the aim of this research. More specifically we aim to invent new robust estimators that can perform more accurately, autonomously and efficiently in practical Computer Vision applications.