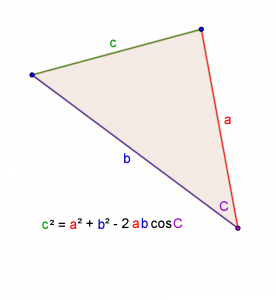
Ever since I first learned it, I’ve always loved the cos rule. It says that if a triangle has two sides a and b, with an angle of C between them, then the remaining side c can be found in this way: c2 = a2 + b2 – 2ab cos C.
The reason I like it is that it’s like Pythagoras’ Theorem, but with an adjustment to make it work out right for non-right-angles. See the c2 = a2 + b2 is Pythagoras’ theorem and the – 2ab cos C is the bit that adjusts the answer to take into account that the angle C is more or less than a right angle.
Anyway, I recently saw Euclid’s original version of the cos rule — and it doesn’t use cos at all!
It goes something like this (this is my version of course — I’m sure Euclid didn’t use this exact turn of phrase):
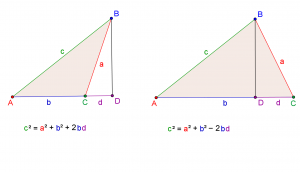
You have a triangle ABC with sides a, b and c opposide their matching angles.
Find the perpendicular from point B to the line b, and label D the point where it meets b. Label d the distance from C to D, and say that d is negative if it’s outside the triangle and positive if it’s inside the triangle.
Then c2 = a2 + b2 – 2bd.
Here’s a diagram of the two situations:
Isn’t that cool? The coolness of it is that it’s all based on the lengths you can construct from the triangle, and there’s no need to make reference to a strange function of angles like cos in order to do it. In fact, all you need to prove it is pythagoras’ theorem, which you can convince yourself is true just using paper and scissors.
Somehow it makes the cos rule — and even cos itself — even more real to know it has such a grounding in the lengths and areas of triangles.