If someone asked you what your favourite 3D shape was, what would you say? A cube? A sphere? A dodecahedron?

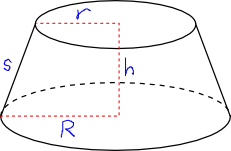
Well, my favourite 3D shape is the frustrated cone. A frustrated cone is a cone with the pointy bit cut off (some people call it a “conical frustum” or a “truncated cone”, but “frustrated cone” sounds so much cuter).

And why is it my favourite?

Well firstly it’s the name. It makes it sound like it has a life of its own — like it wants to be a cone, but has been prevented from making it all the way to the vertex. This is one more example of my general personality-based approach to understanding all sorts of things. Moreover, most people I talk to have never heard the name, and so if I bring it up then I have to explain it, thus extending my opportunity to talk maths.

Secondly, the formulas associated with it are pleasantly simple: the frustrated cone in the picture has a curved surface area of π (r+R)s, and a volume of 1/3 π h (R^2 + Rr + r^2). Aren’t they nice? Moreover, the formulas connect neatly to the formulas for cylinders and full cones: If r=0, then you have a cone and the formulas both give the right answer, and if r=R you have a cylinder and the formulas still give the right answer. That appeals to my mathematical sense of connectedness.

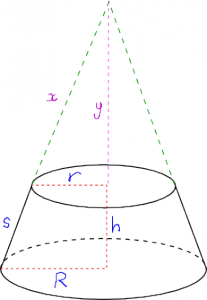
Thirdly, the method for coming up with these formulas is an excellent work of problem-solving. What you do is imagine that your frustrated cone _is_ a bigger cone that has been cut off, and you give a letter to represent the unknown height of the vertex above the top face. Using the formulas associated with a full cone and the properties of similar triangles, you can get the formulas I had before. (I’m not putting the working here because that would rob you of the fun of figuring it out yourself!)

And finally, it just looks cute, sitting there all squat and round like a creme caramel!