One of my staff (thanks Fergus) told me ages ago about Archimedes’ proof that the volume of a sphere is 4/3 π R³ (where R is the radius of the sphere). It is a very very cool proof and it’s high time I shared it! One of the reasons it is so cool is that it uses the concept that a volume can be produced by stacking up a whole lot of thin slices. This is the idea behind integration, and Archimedes used this idea thousands of years before Newton or Leibniz.

So here is a modernised version of the proof:

We’re going to assume we already know a few things:

1. How to calculate the area of a circle.
2. Pythagoras’ theorem.
3. The fact that all the points on a sphere are the same distance from the centre (the radius).
4. The fact that a cone has a third the volume of a cylinder with the same base and height.
5. How to calclate the volume of a cylinder.

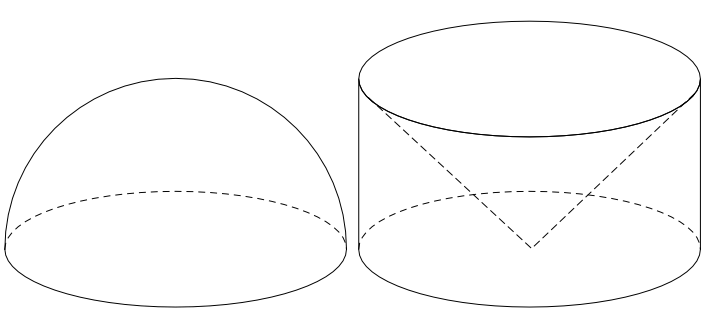
Ok, now let’s get a sphere of radius R and slice it in half to make a hemisphere. Next we’ll get a cylinder of radius R and height R, and we’ll scoop a cone out of it to make a sort of bowl (see the pictures).

The volume left for our cylinder-minus-cone bowl is two thirds of the volume of the cylinder (since the cone is a third the volume of the cylinder). We’re going to show that the hemisphere has the same volume.

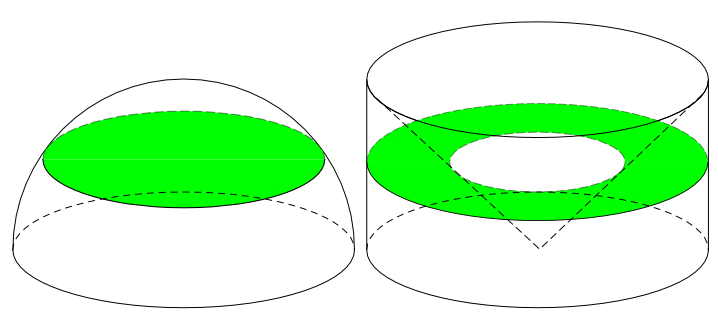
We are going to do this by working our way up from the bottom and slicing both shapes into very thin slices. If we can show that at every possible height the slice for the bowl has the same area as the slice for the hemisphere, then it must be true that the two shapes have the same volume.

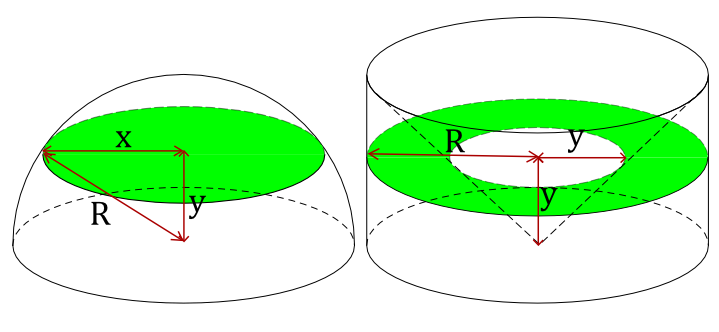
So suppose we are at height y above the base:

Consider the bowl: when we slice the bowl, we will get a circle of radius R with a hole in the middle. The edge of this hole is on the outside surface of the cone. Now a line in the curved surface of the cone has slope 1 (since it goes across R and up R), so since we’ve gone up y, we must also have gone across y to get to the edge of the cone. That is, the radius of the circular hole is y. Hence the area of the slice at height y is π R² – π y².

Consider the hemisphere: when we slice the hemisphere, we will get a circle — let’s say the radius of this circle is x. Now a point on the edge of this circle is a distance x from the vertical centre line of the hemisphere, and it’s a distance y above the base, and it’s a distance R direct from the big centre of the hemisphere in the middle of the base. Using Pythagoras’ theorem, we get that x² = R² – y². But the area of our circular slice is π x², which is equal to π (R² – y²) = π R² – π y².

So the areas of the slices at every height are the same! So when we stack up those areas to produce a volume, the two volumes must be the same!

Since the bowl has two thirds the volume of the cylinder, this means our hemisphere’s volume is also two thirds the volume of the cylinder! Therefore a whole sphere must be four thirds the volume of the cylinder.

Now the volume of the cylinder is the base area times the height, which is π R² * R. So therefore the volume of the sphere must be 4/3 π R³.

How cool is that?!