In first year maths, they briefly study the five families of number: the natural numbers N, the integers Z, the rational numbers Q, the real numbers R, and the complex numbers C. In particular, they focus on the distinction between the rational numbers and the real numbers. A classic proof they are given at this time is one that the number √2 is irrational. Below is how the proof normally goes:
This proof is quite confusing to students, not least because it’s the very first proof by contradiction most of them have ever seen, and the contradiction in this proof comes from something we created ourselves inside the proof — the fact that the fraction p/q is in lowest form. (Admittedly it could work without that, and the contradiction would come from creating an “infinite descent”, but that is possibly even more confusing.)
The other thing that makes it difficult is the use of the fact that if p2 is a multiple of 2 then so is p. This is a number theory concept, due to the fact that 2 is prime, and I feel it’s something that is a bit uncomfortable for students. In class, they skirt around that by saying that if p2 is even then so is p, but I feel that is a bit of red herring, because even-or-oddness would be totally irrelevant when you came to show that, say, √3 is irrational.
I recently learned a couple of other proofs that √2 is irrational, which I think are better than this one, at least pedagogically. The first one is only a little different from the one above, but I think it has some distinct advantages:
This proof neatly avoids the issues that the previous problem creates. Firstly, it doesn’t have the murky “divisibility by 2” issue, which is a bit of a hang-up in the previous proof. It does this by using the concept of cancelling down fractions, which students have to understand in order to understand lowest terms anyway. Finally, the contradiction comes from outside the proof — it’s obvious to most students that √2 can’t possibly be an integer! (Technically we could have used the “fraction is not in lowest terms” contradiction, if we wanted to, but that caused problems last time, didn’t it?).
While I certainly would recommend the above proof pedagogically, I can’t leave this discussion without mentioning the proof that started me thinking about alternatives in the first place:
I certainly wouldn’t use this with students as the first proof that √2 is irrational because it gets its contradiction from inside itself, and most people would wonder how on earth they would come up with it themselves. But it does run by a completely different mechanism than the other two, and only uses a few very fundamental facts about integers, which makes it quite surprising. Its surprising nature is just the sort of thing I’d love to show students, just to point out that the above proofs are not “the” proof that √2 is irrational.
(Note: This proof was inspired by “What Pythagoras could have done”, Yoram Sagher, American Mathematical Monthly, 95 (1988) )

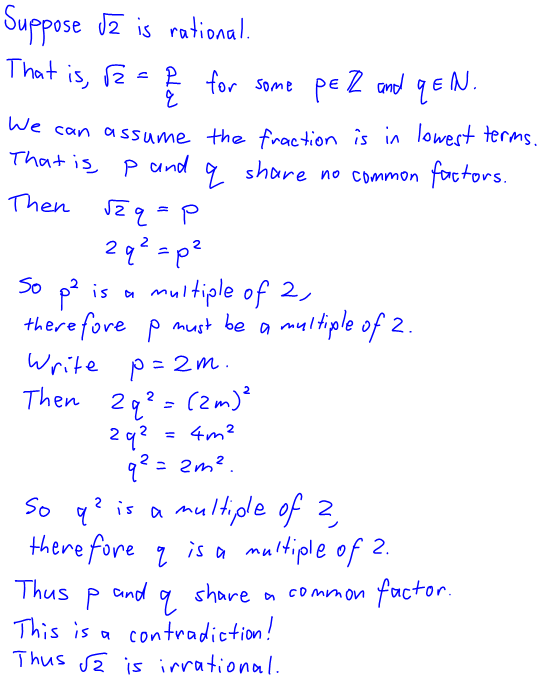
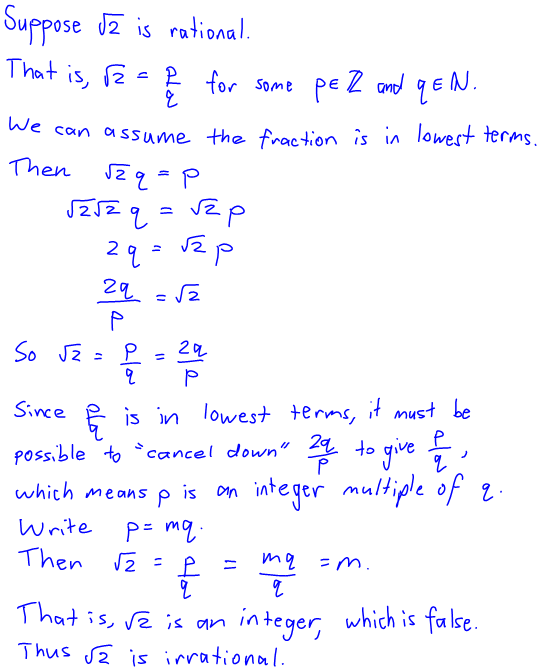

I really like the second proof (though some purists might object that its use of facts about reduction of fractions amounts to a tacit appeal to the fundamental theorem of arithmetic that makes the proof less elementary than the other two). For one thing, the second proof readily generalizes to show that for all positive integers n, not just n=2, the square root of n cannot be rational unless it is an integer. Nice!
Yes I rather liked that you could use it to show that square roots can only be rational if they’re integers.