It’s no secret that the powers of two are some of my favourite numbers. There are so many interesting things to say about them that often I don’t know where to begin! (In case you’re not au fait with the terminology, the powers of two are the numbers you can make by starting with 1 and multiplying by 2 over and over. The list starts out 1, 2, 4, 8, 16, 64, 128 etc.)

Well, the other day, one of my staff (thanks Lyron) reminded me of one of my favourite facts about the powers of two. I like to call this fact “The Sausage-Stacking Theorem”.

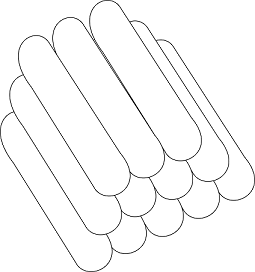 First I need to set up the situation. Imagine a nice neat stack of sausages. It has a row of sausages on the bottom layer, and another row on top of that with one less sausage because they sit in the furrows between the sausages on the bottom layer. There may be other layers on top of this, each with one less sausage than the layer below.

The Sausage-Stacking Theorem is this:

A power of two sausages cannot be arranged into a nice neat sausage stack.

No matter how you try, it simply can’t be done; there will always be sausages left over or not enough sausages to fill in the top row. (In mathspeak, you could say that a power of two cannot be written as the sum of two or more consecutive natural numbers, but the sausages are cuter.)

What Lyron encouraged me think about was a way to prove this theorem without resorting to the usual mathematical notation a trained mathematician like me would normally use. Well, using the proof he showed me as inspiration, I have come up with something that is strongly visual, and it goes like this…

Consider a number of sausages that can be made into a nice neat stack. We’ll show that it must be possible to divide this number evenly by an odd number. We’ll split it into two cases: if the stack has an even number of layers or if the stack has an odd number of layers.

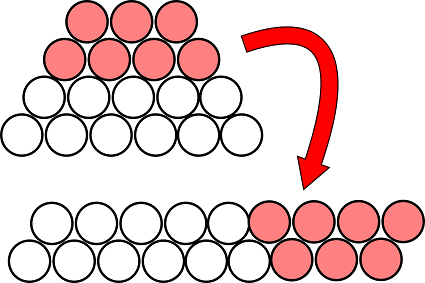Suppose the stack has an even number of layers (my diagram has four, looking end-on). Imagine removing the top half of the layers, flipping them over, and joining them to the rest of the stack. (I say “imagine” because you’ll need the sausages to hang in mid-air to do this physically.) Now you have a parallelogram made of several layers, each with the same number of sausages. The number of sausages in the bottom layer was made by joining the bottom layer and the top layer of the original stack. Since the original stack had an even number of layers, the top and bottom layer are an even number and an odd number. So when you add them together you’ll get an odd number in total. Thus the new parallelogram stack has several layers, each with the same odd number of sausages. So, it’s possible to divide the total number of sausages by this odd number.

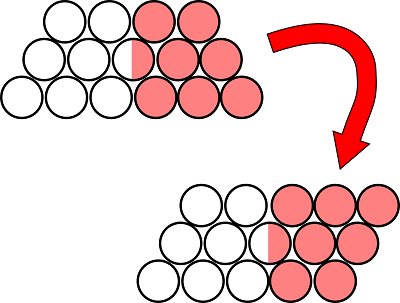Now suppose the stack has an odd number of layers (my diagram has three). Imagine slicing your sausage stack down the centre, flipping one side upside-down and sticking it back on. Because there are an odd number of layers, the half-sausages will join together neatly and you’ll get a parallelogram made of several layers, each with the same number of sausages. There are still an odd number of layers, so it’s possible to divide the total number of sausages by this odd number.

So in either case, it’s possible to divide your number of sausages by an odd number. A power of two can’t be divided by any odd numbers at all, so it can’t possibly be the number of sausages in a nice neat stack.

How cool is that?!