There are two terminologies in probability which many students are confused about: “independent” and “disjoint”. The other day I was working with a student listening to their thinking on this and I suddenly realised why.
In your standard introduction to probability notation, various notations and terminologies are introduced, usually with reference to the meaning of the English words and also with reference to Venn diagrams. Here is a streamlined version:
When I laid it all out like this, I noticed something most interesting: In every notation and terminology except “independent”, the meaning of the English word related directly to the shape of the Venn diagram. Independent related only to the abstract meaning of the word and not to any property of the Venn diagram at all!
When a student is learning probability, we actually tell them to use the Venn diagram to help them know the meaning of the probability terminology. When they get to “independent”, they simply do what we taught them to do. They look at a Venn diagram and they think of an arrangement of the circles which says “independent” to them. My student the other day said, “Well, independent means not reyling on each other, so in the picture that would have to be two circles that don’t touch.” But of course, the English meaning of the word independent doesn’t describe how a Venn diagram looks when events are statistically independent! In some sense, we’ve set up our students to fail!
But what are we to do about it?
Well, I have a few ideas.
Firstly, do what I just did and line up all the definitions. Then it’s much more clear that independent doesn’t have a direct link to the Venn diagram. It certainly worked for me!
Secondly, make Venn diagrams to illustrate what independent does look like. Basically, A and B have to overlap in a very specific way in order to be independent. I don’t recommend using circles because it’s too hard to see the specific relationship between the areas. (In general I don’t like circles for Venn diagrams actually.) This seemed really to help the student I was working with that day.
Finally, to find out if your students understand, give them a task to do. I gave this one to a third-year statistics student, and it highlighted that he still had the picture for disjoint in his mind, even though he knew the formal definition of independent.


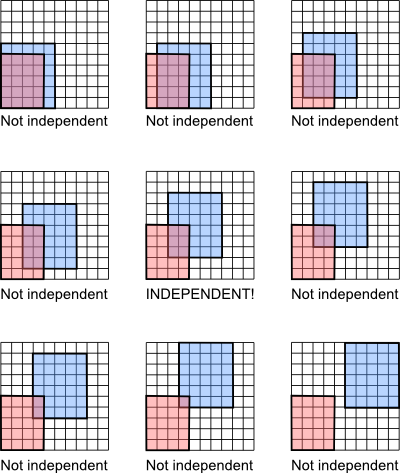

Wonderful visual and added commentary David. Just what I need for my Grade 10 High School students.
So glad it was helpful to you!
I really like this posting. I agree with your thesis that we sometimes set up our students to fail. Venn diagrams are useful but can some characteristics confuse for students. I have a question.
You state “Independent related only to the abstract meaning of the word and not to any property of the Venn diagram at all!” Isn’t independence a property of Venn diagrams? You even demonstrate this in your grid example. To be independent the fraction of the total area that overlaps needs to equal the product of the fraction of the area of the two pieces forming the overlap. However, what is true is that it is difficult to see this using circles in Venn diagrams. Your grid Venn diagram shows it very nicely. Am I just misunderstanding this?
Thanks.
In a traditional Venn diagram, the areas of the spaces are irrelevant, only the way they overlap is important. In order to show independence, I’ve had to add an extra feature of area being proportional to probability, which wasn’t a feature of the original Venn diagrams. All the other terminologies are showable in a Venn diagram without reference to the areas of the parts.
Also in the statement you quoted I wasn’t saying that you can’t represent the property independence in the picture. I saying that the NAME “independent” isn’t a natural language description of the PICTURE of the Venn diagram. Even with areas, the ordinary English meaning of the word independent still doesn’t really have much to do with the way the areas are related in the picture. The point I was making is that the SHAPES in the pictures couldn’t be said to be independent in a naive natural way.