This is the second in a series of posts about the Maths Day I did in my daughter’s Year 7 classroom. Last time, I talked about the awesomeness of the day as a whole. For the next few posts, I’ll talk about the actual activities we did.
After the general intro into me and what I do, we launched straight into Quarter the Cross. This is one of my favourite problems ever, and you can read all about my love affair with it here. As I said there, it has so many opportunities for mathematical thinking and creativity. Yet the big question on the lips of several educators on Twitter is “How do I implement it in a classroom.” Well, here’s how I did it.
Launch
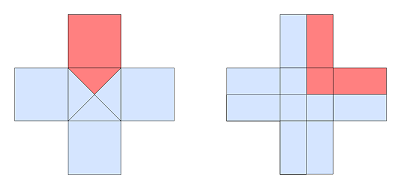
I started out by showing the puzzle on the screen:
I told the students they could use whatever method they liked of quartering the cross, including drawing lines with rulers or cutting them out. The important thing was that they could explain how they knew it was a quarter. I said I would be looking for some people to share their solutions with the whole class.
We gave everyone a sheet with five of the puzzles on it in white, telling them they could always get more or draw their own. Then I gave them 10 minutes to play with it on their own, after which we’d stop to talk about it as a class. While they worked on it, we circulated and talked to the students about what they were doing. Even though we said they had to do it on their own, we didn’t tell them off for discussing with people around them quietly.
First try
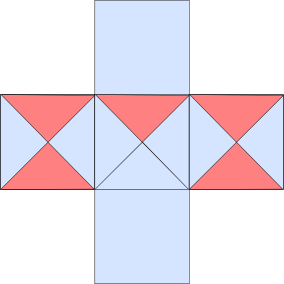
When I was with the students, I was specifically looking for approaches that we could share as a whole class. In my experience, most people do the following two solutions first:
I was not disappointed. Almost everyone had one or both of these. I asked a couple of students with these solutions if they’d be ok with sharing theirs with the class. I also looked out for several other interesting solutions that I thought would inspire other students or have something cool to talk about, asking some more students if I could call on them too. Then we stopped the class and had a whole-class discussion.
Whole-class discussion
Now we called a whole-class discussion, I called upon the students I had picked to share their solutions and explain how they knew they had a quarter. They showed their solutions on the document camera (the teacher Anne called it a “hovercam” which was a new word for me) so that everyone could see it on the screen.
The first solution was the house-shaped one I showed earlier. The first student explained how there were four squares and one left over, so they took one square and a quarter of the middle one. I asked for a show of hands to see how many people had this solution (pretty much everyone). Another student had done this one, but literally cut the cross into quarters, and I asked him to show how the four identical pieces fit together to make the whole cross.
The second solution was the L-shaped one I showed earlier. Again I had two students show their solutions: one student had drawn it on paper, and another student had actually cut it out and folded it twice. I said how much I loved that there were multiple explanations, and this set the tone for what followed.
Now I called upon the other students I had picked out. They brought their solution out and showed it on the camera, and explained how it worked. Several times I asked other students if they had an alternative explanation of why it really was a quarter. One student explained how you could show his was the same as the first one by literally cutting a bit off his and fitting it back together again. I was proud of my daughter Kaylee for being brave to show her solution, where she had divided all the squares into 16ths and coloured a random four of each of them. After I had exhausted the people that I had pre-selected, I called on anyone else to share one if they wanted.
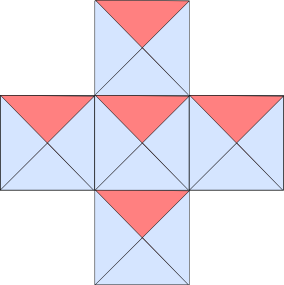
There was one particular solution that generated five different explanations. We had just done this one:
And a student put his hand to ask if this one was ok:
I asked the rest of the class what they thought. One student after another came up to the screen to explain why it really was a quarter. Several of these had to do with rearranging the pieces to fit into our original house-shaped solution. One student (who had been struggling to make his own solution earlier) came up and blithely explained it must be a quarter because you could move this one here and this one here and it was the same as the previous solution, which was still on the screen too. I was so proud of him, and pointed out to the class how this meant we could relate any solution to an earlier one to be sure it was a quarter. The final explanation was along the lines of “It has to be a quarter of the whole cross, because it’s a quarter of each square separately”. I asked the students if they thought that was a general rule, and they all seemed to agree. By now we had quite a crowd of students out the front, and Anne told me later that the student she was with had whispered to her at this point “If this goes on much longer, we’ll all be out there!”
Second try
I don’t really know how long this middle part went on, but after everyone had shared what they wanted to, I asked them to see if they could make some more solutions, based on the inspiration they had seen in the other students’ solutions. I asked them if they could make it look surprising or so it didn’t feel like a quarter. It’s a testament to how engaging this activity was that several of them had actually already started making more solutions while they were listening!
This time we encouraged them to talk to each other, and talk to each other they did. Many students went up to one of the presenters and asked them again how they did what they did so they could try it themselves. Some students wondered about doing thirds, and I had a most productive discussion with them about how to divide a square into thirds. One student realised that to make one whole square you could have any two pieces as long as they fit together to make a full square. One decided to divide the cross into any old pieces and then divide each of those into quarters. In short, it was really quite a fabulous time of maths and creativity.
The end (for now)
Our investigations took us into recess, and after recess I talked to the whole class again. I said that I wanted something to display on the wall so people would see what we’d been doing. So I gave out big versions and asked them to pick a favourite solution and do it big to go on the wall. We encouraged them to look at the other solutions people had done at the same time. (We also gave them some other puzzly activities to do when they had finished that to keep them occupied — this was when we did the Zero Zeros problem.)
Here you can see the collection of solutions that we put on display:
Some thoughts
I am really proud of how this went. In many ways it was the perfect way to start. The problem is straightforward enough to get into quickly, and had that wonderful opportunity to allow students success in presenting their explanations. Plus it produces something pretty to go on the wall: as we all know, leaving artifacts behind is an important part of learning!
If I were to do it again, I would make sure my handouts had squares a whole number of centimetres wide. Then they would have been able to more easily divide the edge into fractions of their choosing, plus reinforce some other skills too. On that note, here is the small version with five crosses, and here is the big version with one cross, both with a whole number of centimetres for the squares’ sides.
Also, if I had more time, and an inclination to do so, I would probably get students to start representing some of what they see with equations involving fractions. Things like 5/4 = 5*1/4 and 5/4 = 1/2 + 3/4.
In the end, though, I was so happy with what we achieved on the day.
Epilogue
When we got home that night, my daughter Kaylee kept working on the Quarter the Cross, investigating many different ideas she never got to during the day. My younger daughter Charlotte wanted to join in too, and we made several solutions together which were built from cutting the cross in half and half again, then cutting the solutions we had up and arranging them differently. (Charlotte did a big one too, which Anne graciously put up with the others on her class pinboard.) I don’t know what happened in other households, but in mine there were several hours of mathematical play that this inspired outside of class.
Of course, causing hours of mathematical play is my usual experience with Quarter the Cross 😉 .
PS: Here are the rest of the posts in the series:
- How I felt about the day
- Quarter the Cross
- Zero Zeros
- Spotless Dice
- Mathematical art appreciation
- Hotel Infinity
- Thanks for coming



There are still many conversations that happen between the students around the display board, discussing and justifying “the quarter!”
The activity uncovered misconceptions about fractions and raised the question about when it is important to be accurate, and when near enough is good enough.
Loved this activity!
So glad they are still talking about it. It makes me happy that it has fueled so much interest, and so much learning in the longer term.
[…] how I implemented Quarter the Cross […]
[…] how I implemented Quarter the Cross […]
[…] talked about my feelings about the day overall, and all but one of the activities we did: Quarter the Cross, the Zero Zeros, Spotless Dice, and looking at my maths art. In the timeline of the day, we are now […]
[…] Quarter the Cross […]
[…] Quarter the Cross […]
[…] daughter’s Year 7 classroom. I started back with The Best! Day! Ever! and then talked about Quarter the Cross. This post is about a puzzle I gave to students to fill in some time while their classmates […]
[…] I have quite a love affair with the Quarter the Cross problem, having blogged about it here and here. This blog post is not about Quarter the Cross, but the story did start […]
[…] I wrote a later post on how I implemented this in a classroom. Over there I have links to the Word documents with blank crosses to print for students, but you […]
[…] that a lot of people have so that everyone can get buy-in to the discussion (I did this when I did Quarter the Cross in my daughter’s classroom). You might want to start with a solution containing a misconception to get it out of the way. You […]
[…] the Australian blog where I first read about this task, this is one of the most common first […]
[…] was really excited to try this challenge in my classroom. For the first lesson, I followed the lesson outline that David Butler described in his blog. I gave out the templates with the crosses, the students […]
I am so happy for sharing useful information about math. Life is a mathematical problem. To pick up the most, you need to realize how to change over negatives into positives. I will be back again to check and read more of your post. Thanks!