This post is the sixth in a series about a Maths Day I did in a Year 7 class last week. I’ve talked about my feelings about the day overall, and all but one of the activities we did: Quarter the Cross, the Zero Zeros, Spotless Dice, and looking at my maths art. In the timeline of the day, we are now under an hour to go until hometime. It’s time for a calm sort of activity. In short, it’s story time!
The Story
When I was a high-school teacher in training, I happened upon a story called “Welcome to Hotel Infinity” by Nancy Casey. It used to be hosted on the MegaMaths website along with some ideas on how to use it in your classroom, but that website no longer exists. The story itself can be found in PDF form at this link.
It’s a very nice little story about a man who builds a hotel with infintely many rooms and a fleet of busses with infinitely many seats, in a world where there are infinitely many people to fill them. It has all the features that make such a story engaging: charming characters, thoughtful little details, a bit of tension and quite a bit of heart. Plus the characters have their names based on some of key players in the real history of infinity. I loved it so much I made a t-shirt based on it, with this picture:
Since then, I have seen other stories on the same theme, and even heard about the supposed original concept of “Hilbert’s Hotel”. (It is possibly midly shocking that I never heard of “Hilbert’s Hotel” during four years of an honours maths degree.) None of these, including any discussion of Hilbert’s Hotel, have ever come close to the charm of Nancey Casey’s story.
The lead-in
We were on the floor looking at maths art already, so I took the opportunity to show a bit of M.C. Escher’s artwork. I didn’t mention that it had anything to do with what would happen next, I just said it was some cool mathematical art. We looked at them and discussed what was possible and impossible, and how he managed to fit more into his pictures than could physically fit.

Reading the Story
After this look at these impossible pictures, I said I would be reading them a story. This was sort of convenient because their teacher Anne normally does read to them in the afternoons. Today was different though, because I gave them all paper and asked them to illustrate what they heard if they wanted to.
And then I read the story. I moved to a more central place in the room and read it from start to finish. It took me about half an hour. Note that I have read this story several times, and also I am a fast reader even when I’m deliberately trying to go slowly, so if you try this perhaps give yourself a little longer!
Hardly anyone chose to illustrate the story as I read it. When I did this with my Year 7 class back in 2003, almost all of them chose to illustrate the story and we had the most fabulous illustrations. This time, pretty much nothing. Go figure. Now that I write it, I remember that when I did this in my own class, I told them they could also write down any questions or thoughts they had about the story as they thought them. I didn’t tell Anne’s class to do that, which was a missed opportunity I feel. Oh well.
This is an appropriate place for some favourite quotes:
From then on, more people came than left every day, so the hotel was always full. We used the loudspeaker to get everyone to move down whenever we needed an extra room. It got to be known far and wide that this would happen, and people began coming to the hotel just to see how many different rooms they could get to stay in. They might start out in an upstairs room with dinosaurs on the wall paper, and then the loudspeaker call would come, and they would have to move to the room with the checkerboard bedspreads. If it was a particularly busy day, a lucky family might,
all in one day, get to stay first in the room with the elephant-shaped bathtub, then in the one with jungle plants and trapezes. After dinner they might get sent to the room that has the bathtub slide, and end up going to sleep in the one with the fold-down beds. People didn’t mind moving. That turned out to be half the fun. (page 6)There are ways, Mr. Kronecker, that you could prove that what Mr. Cantori claims about his hotel is not true. If there aren’t infinitely many people there, as you claim, just count them and tell us how many there are really. (page 6)
How can there be more than infinitely many people on those busses? (page 9)
Question time
When the story had finished, I asked anyone if they had any thoughts. I didn’t try to lead them in any particular direction, but just applauded their noticings and answered their questions as honestly as I could. Often the answer was a question along the lines of “Well, what do you think?”:
Some of my favourite questions and comments were the ones about how there couldn’t possibly be infinitely many people in the hotel, since there are only seven and a half billion people on earth, which is big, but certainly not infinite. There was talk about how could you get infinitely many people into the hotel, since surely that would take an infinite amount of time? There was also quite a lot of talk why moving people into the even-numbered rooms leaves infinitely many rooms empty, and why that’s even necessary. That is, if you can get people to move down one or two or a hundred rooms, why not infinitely many? In the end we moved on to talk about other infinite things like the decimal expansion of 1/3 and of pi. We even briefly talked about how there were different sizes of infinity and how there are just as many fractions as whole numbers.
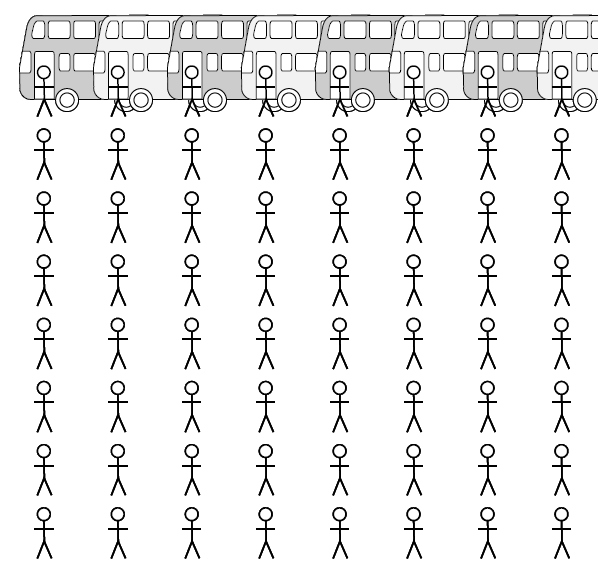
Actually, that one’s worth mentioning in more detail, because the story itself really helped there. There’s this scene where infinitely many buses all turn up, each with infinitely many people on it. How do you fit everyone into the hotel? Here’s the description from the story:
“OK,” I said. “Now, we’ll take the first person off the first bus and the first person off the second bus.” A lady with a briefcase. A man and his dog. No problem. “Now, we get the next two people off the first bus, one person from the second bus, one person from the third bus, and one person from the fourth bus.”
You know, people who come to the Hotel Infinity are all so wonderful. Other folks might have minded the wait, but these people were cheerful, like it was a game. People who came to the Hotel Infinity counted on doing something unusual.
After the first person got off the fourth bus, we worked our way backwards, taking one person off the third bus, the second bus, and the first bus. Then one more off the first bus, and we worked our way back up, taking one person from each bus that was already in the game, and adding a person from the fifth bus and a person from the sixth bus this time. Back and forth we went, always letting two people off the first bus, and starting to empty two more busses each round.
This is not particularly easy to follow on the first glance! When a student asked, I said that I too had trouble following that, and it really helped to draw a picture. I drew a picture like this on the board:
Then I started drawing a line showing the people who went onto the bus and in what order. The line forms a very neat zigzag back and forth. It’s quite beautiful, and it does show that you will get to everyone eventually. One student wasn’t convinced that it was possible to really have infinitely many lists of infinitely many things, and I said that the fractions are infinitely many lists of infinitely many things. The student didn’t believe me, so I used the people on the buses to show it. I labelled each person on the first bus with a fraction with denominator 1. The second bus had denominator 2, the third bus had denominator 3, and so on. This student and many others this demonstration of the structure of the set of fractions.
The End
Suddenly, it was time to wrap up because the end of the school day was imminent. I wanted to leave one parting shot, so I said that to me, this is what maths is really about. It’s about ideas. Some ideas are so interesting that people have thought about them for thousands of years. Infinity was a topic of study in ancient Greece and ancient India and people still study aspects of it today. Really, with mathematics you can never be bored, because there’s always something interesting to think about.
PS: Here are the rest of the posts in the series:


[…] Hotel Infinity […]
[…] Hotel Infinity […]
[…] Hotel Infinity […]
[…] Hotel Infinity […]
[…] Hotel Infinity […]