The story so far
I promised Tina on Twitter that I would write about how the line at infinity relates to conics, and I’ve been doing it in the last two blog posts.
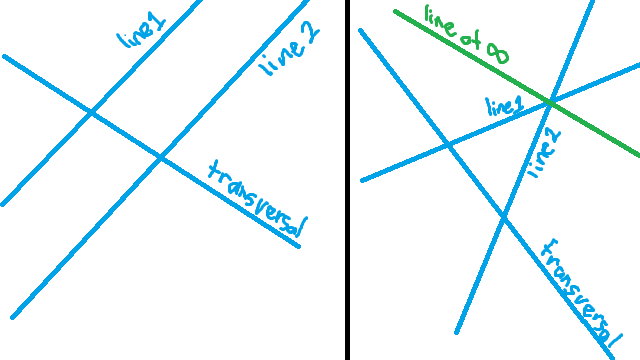
First, I talked about what the line at infinity is. We noticed that a set of parallel lines all share a slope, so we elevated all the slopes to the status of points and gave them a more physical reality as “points at infinity”. Now lines we thought were “parallel” aren’t anymore because they actually meet. Any two lines meet, though possibly at a point at infinity.
Second, I talked about a system of coordinates that includes the line at infinity. It turned out we could do this by giving both points and lines three coordinates, with the understanding that any nonzero multiple of a set of coordinates represents the same point/line.
These coordinates are called homogeneous coordinates and they go like this: Points have coordinates of the form (x,y,w). Ordinary points have w not equal to zero, and their original coordinates can be calculated as (x/w, y/w). Points at infinity have w equal to zero, and a point of the form (a,b,0) is the point at infinity belonging to all the lines parallel to bx – ay = 0. Line equations go from ax + by + c = 0 to ax + by + cw = 0, which can be shortened to coordinates [a,b,c]. The line at infinity has equation w=0.
New perspectives from homogeneous coordinates
Last time I noted how awesome it is that with these new coordinates, lines and points are not really distinguishable from each other, if we just look at their coordinates. There is another thing I think is very cool too: with these new coordinates, the points at infinity don’t look fundamentally different from ordinary points. So what if one of their coordinates is zero? Other points have a zero coordinate, such as all the points on the x-axis — they have coordinates of the form (x,0,w). The line at infinity has equation w=0, but that’s not really any different from y=0. If I try not to think about where it is, and just focus on the coordinates, then the line at infinity is not different from any other line.
If we want to, we can think of this like magically travelling to stand on the line at infinity, and from that perspective it looks just like any other line. Interesting things happen when you shift perspective this way. For example, consider two parallel lines and a transversal: if you stand on the line at infinity, you can see the point at infinity involved, and the three lines become just an ordinary triangle. We’re going to talk about what happens when you do this to conics.
Conic (sections)
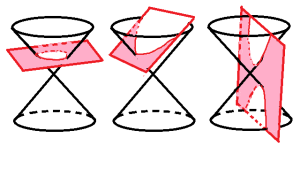
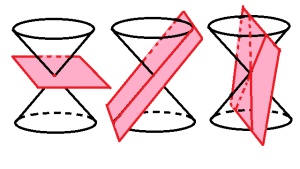
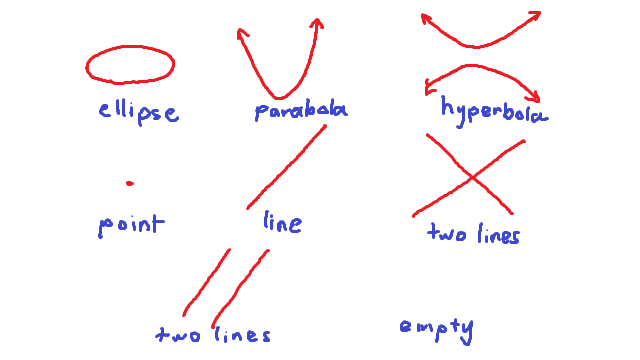
Conics began life millenia ago as literal sections of a cone. You took a circular cone, including both a top nappe and a bottom nappe, and you sliced it with a plane at various angles to produce various results – parabolas, ellipses, hyperbolas. If you arranged it just right, you got a point, or a single line or a pair of lines. These are often called the “degenerate conic sections”.
Later, when coordinate geometry became a thing, it turned out that the conic sections could be described as the set of points whose coordinates satisfy a quadratic equation. Take a quadratic equation in two variables like x2 – 3xy + y2 – x + 4y – 7 = 0, and find all the points that work when you sub their coordinates into the equation and this give you a conic section. Very nice.
There are a few extra possibilities that appear from our equations that aren’t covered by our cone: a pair of parallel lines, and an empty set where no points at all satisfy the equation. To include these, we’ll drop the word “section” from the name, so that they’re still objects related to cones in some roundabout way, but not necessarily a section of a cone.
Quadratic equations in homogeneous coordinates
When we introduced a third coordinate to our points, and so introduced a third variable to our lines, we simply attached our new variable to the constant term in our line equation. Like this: 3x – 7y + 5 = 0 becomes 3x – 7y + 5w = 0. But it’s not so simple with quadratic equations. In fact, it’s just the slightest bit dodgy to simply attach a w to the constant term, because the x and y in the first equation aren’t really the same as the x and y in the second equation if w isn’t 1. A more rigorous approach would be to remember how to convert from three coordinates back to two like this: (x,y,w) becomes (x/w, y/w). So that “x” in the first equation is actually x/w, and the “y” is actually y/w. Then 3x – 7y + 5 = 0 becomes 3(x/w) – 7(y/w) + 5 =0, and multiplying by w gives 3x – 7y + 5w =0.
(Someone is sure to notice the slight dodginess here too: I’ve still used x and y to mean different things before and after the change. My geometry lecturer back in the distant past switched to capital letters to mark the change, but I think we’ll cope with just a little bit of notational sloppiness for the ease of explanation. I hope so anyway.)
This is how we’re going to deal with quadratic equations. That is, we’ll replace the x’s with x/w and the y’s with y/w:
x2 – 3xy + y2 – x + 4y – 7 = 0
(x/w)2 – 3(x/w)(y/w) + (y/w)2 – (x/w) + 4(y/w) – 7 = 0
x2/w2 – 3xy/w2 + y2/w2 – x/w + 4y/w – 7 = 0
x2 – 3xy + y2 – xw + 4yw – 7w2 = 0
(To get to this last line, we multiplied by w2.)
So the linear terms get a w attached to them, and the constant term gets a w2. This has the effect of meaning that in every term there are two variables multiplied together, either two different ones like xy or yw, or two of the same like x2 or w2. All the terms are the same in some sense now — homogeneous, as it were.
How conics meet lines
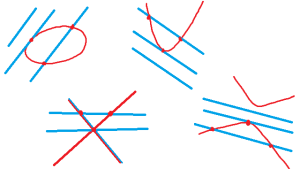
We’re now ready to figure out how our conics meet the line at infinity. Well, nearly. First it’s probably a good idea to know how conics meet ordinary lines! Drawing some pictures, I can convince myself that a line either misses a conic entirely, meets it in exactly one point, meets it in exactly two points, or (in the case of some degenerate conics) is actually part of the conic itself.
The algebra matches the drawings (as it ought to). For example, take a line equation in our old coordinates like 2x + 3y – 7 = 0 and a quadratic equation in our old coordinates like x2 – 3xy + y2 – x + 4y – 7 = 0. You can rearrange the line equation to get y in terms of x, and sub that into the quadratic equation to get a quadratic equation in terms of just x. And a quadratic equation has zero, one or two solutions, corresponding to zero, one or two points where the line meets the conic. The only other possibility is when everything cancels out in which case every x is a solution and the whole line is part of the conic.
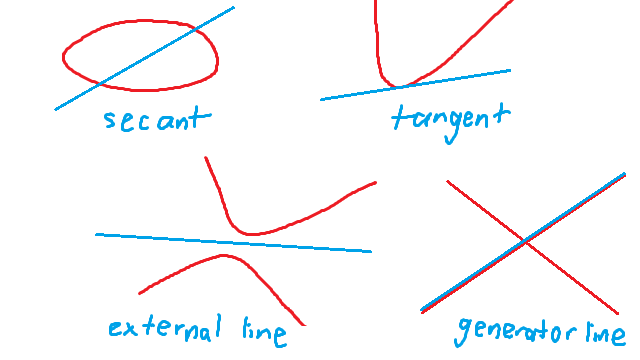
There’s some terminology to name the different kinds of line with respect to a conic. If the line misses the conic entirely, we’ll say “the line is external to the conic”, or say “the line is an external line”. If the line meets the conic in exactly one point, we’ll say “the line is tangent to the conic”, or say “the line is a tangent”. And if the line meets the conic in two points, we’ll say “the line is secant to the conic”, or say “the line is a secant”. (And if the line is actually part of the conic we’ll say “the line is a generator line of the conic”, but that’s not going to come up for our line at infinity.)
A story about me: My PhD thesis was mostly concerned with tangents, secants, generators and external lines of conics and their higher-dimensional friends and relatives, so these words bring back all sorts of memories for me. In particular, I remember giving my second-year thesis seminar the title “David Butler and the Chamber of Secants”. (The first-year seminar was called “David Butler and the Philosopher’s Cone”, by the way.)
How conics meet the line at infinity
Ok, now we’re ready to find how our conics meet the line at infinity. Let’s try the conic I’ve been using as an example so far. Its equation is x2 – 3xy + y2 – x + 4y – 7 = 0, and in homogeneous coordinates this is x2 – 3xy + y2 – xw + 4yw – 7w2 = 0. The line at infinity has equation w=0, so let’s sub this in to get x2 – 3xy + y2 = 0. If we treat x as a constant, this is a quadratic equation in y, so we could complete the square/use the quadratic formula to get y = [3x ± √(9x2 – 4x2)]/2. Note the x2‘s under the root sign which mean we can pull it out, and indeed pull the x’s right out to get y = x [3 ± √5]/2. So we have two points at infinity of the form (x,x[3 ± √5]/2,0). We can divide by the x to get (1,[3 ± √5]/2,0), which looks a bit nicer. And actually, this means that the points at infinity on this conic are the same as the points at infinity on the lines with slope [3 ± √5]/2.
This is all well and good, but it’s not particularly edifying is it? No, not really. Perhaps it might be best to do this trick with our standard versions of the three non-degenerate conics. That might be a bit more illustrative. I’ll do them in this order: hyperbola, parabola, ellipse.
Hyperbola
Your standard form of a hyperbola equation looks like this (x/a)2 – (y/b)2 = 1. In homogeneous coordinates this is (x/a)2 – (y/b)2 = w2. When we sub in w=0 we get
(x/a)2 – (y/b)2 = 0
(x/a)2 = (y/b)2
±x/a = y/b
±xb/a = y
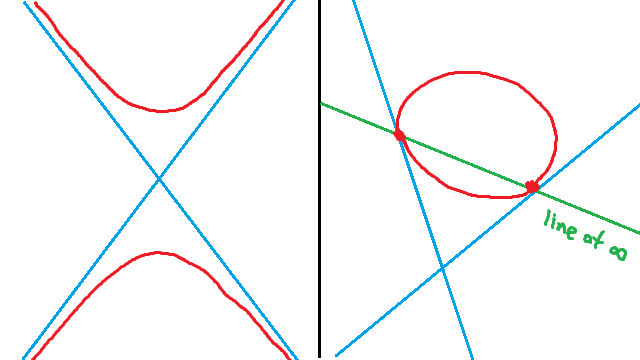
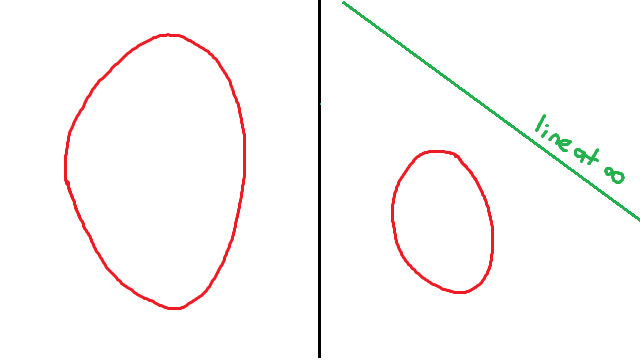
So our hyperbola meets the line at infinity at (x, ±xb/a,0) = (1, ±b/a,0). That’s two points, so the line at infinity is secant to our hyperbola. Interestingly, those are the two points at infinity on the lines with slope ±b/a. If you happen to know a lot about hyperbolas, these happen to be the slopes of its two asymptotes!
Actually, let’s just check that shall we? The two asymptotes of the hyperbola with equation (x/a)2 – (y/b)2 = 1 have equations y = (b/a)x and y= -(b/a)x. In homogeneous coordinates, we have (x/a)2 – (y/b)2 = w2, y = (b/a)x and y= -(b/a)x. Subbing y=(b/a)x into the conic’s equation gives
(x/a)2 – (y/b)2 = w2
(x/a)2 – ((b/a)x/b)2 = w2
(x/a)2 – (x/a)2 = w2
0 = w2
w=0
So this asymptote meets the hyperbola at a point on the line at infinity. I suppose this makes sense — the conic gets closer and closer to the asymptote, so it only makes sense that they actually meet at infinity.
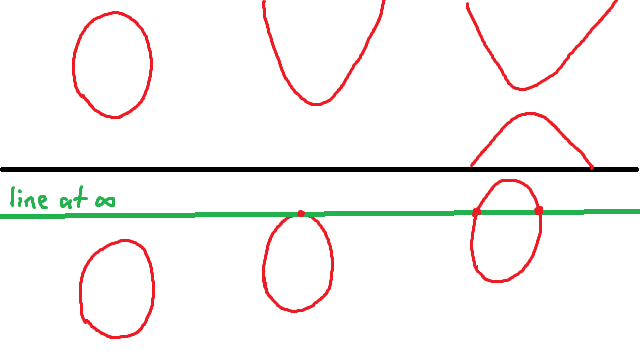
It’s interesting to note that the asymptote meets the conic in exactly one point (x, (b/a)x,0) = (1, b/a,0). That makes it a tangent. Also, even though the two branches of the hyperbola both approach the asymptote, there is only one point where they meet. That does make sense — way back in the first post, we figured out that the point at infinity on any line is both behind and in front of us. If we imagine standing on the line at infinity, you’ll be able to see this point where the conic meets the asymptote. One branch of the hyperbola meets this point on one side, and the other branch meets it on the other side. So here at infinity, the hyperbola links up to itself, like an ellipse.
Parabola
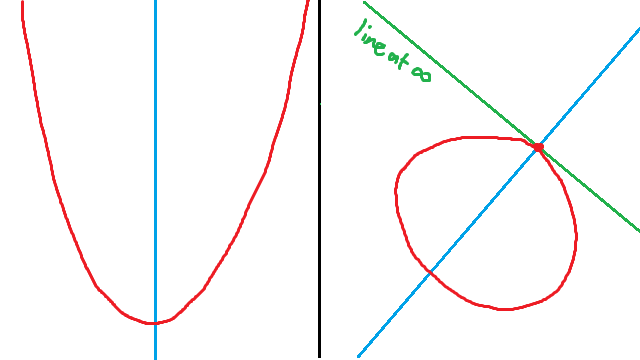
Your standard form of a parabola equation looks like this: y=ax2. In homogeneous coordinates, this is yw = ax2. When we sub in w=0 we get 0=ax2, so x=0. This gives us one point (0,y,0)=(0,1,0). So the line at infinity meets our parabola in one point — it’s a tangent. Interestingly, this is the point at infinity on the y-axis, which is the axis of symmetry of the parabola.
Let’s check this with another parabola. What about x = ay2? In homogeneous coordinates, this is xy = ay2. When we sub in w=0 we get 0 = ay2, so y=0. This gives us one point (x,0,0)=(1,0,0). So again we get one point, this time the point at infinity on the x-axis, which is again the axis of symmetry of the parabola.
Admittedly, this is only two examples, but I’ll trust for a moment that it works. If I do trust it, it seems if I stand on the line at infinity, it’s tangent to the parabola, and the parabola links up to itself at that spot, like an ellipse.
Ellipse
Your standard form of an ellipse equation looks like this: (x/a)2 + (y/b)2 = 1. In homogeneous coordinates this is (x/a)2 + (y/b)2 = w2. When we sub in w=0 we get (x/a)2 + (y/b)2 = 0. Since we can’t have both x and y being zero, this means (x/a)2 + (y/b)2 has to be a strictly positive number, so we have no solutions to this equation. In short, our ellipse doesn’t meet the line at infinity at all. If you like, the line at infinity is external to our ellipse. I suppose this makes sense — we can see the whole ellipse just fine so it shouldn’t meet the line at infinity.
Only one conic
So it turns out that there is actually only one kind of nondegenerate conic. Hyperbolas and parabolas are really just ellipses that meet the line at infinity in different ways. A hyperbola is an ellipse that has the line at infinity as a secant, and a parabola is an ellipse that has the line at infinity as a tangent. I often imagine it as an ellipse that is stretched out further and further, until it meets the line at infinity to become a parabola, and then crosses the line at infinity to come in on the other side as the opposite branch of the hyperbola.
And I think that might be enough. Except for one parting shot — if we have a random quadratic equation, we have a good chance of knowing what kind of conic it is by seeing how it meets the line at infinity. Our original conic with equation x2 – 3xy + y2 – x + 4y – 7 = 0 met the line at infinity in two points, so I can be pretty sure it’s a hyperbola. It is possible it’s actually a pair of lines, I suppose — a pair of lines also meets the line at infinity in two points. There is actually a way of telling the difference, which involves making a matrix and calculating its determinant. But that’s another story and shall be told at another time.

[…] us to define objects using equations. We’ve already defined our lines using equations. The next kind of object is a conic, which is very very […]
[…] next post in the series is all about coordinates, and the one after that is about […]
Hi there,
Fantastic write up, almost has Feynman flavor to it.
Could you please explain how you could arrive at the following conclusion?
“So here at infinity, the hyperbola links up to itself, like an ellipse.”
Are you using the fact w appears as a squared term and that the resulting picture will be symmetric about w = 0?
From your first write up, I got the impression that the point at infinity is the terminus of any ordinary line. In that sense, the point at infinity was the last point on the line. Is this approach correct? If it isn’t and the line keeps going after the point at infinity, what are the points beyond the point at infinity called? I ask this because you draw an ellipse for the hyperbola beyond the line at infinity. In that case, what are those points called? Also, if such points do exist, is it possible that lines at infinity (plural) exist and are parallel? If so, where do parallel lines at infinity meet?
Appreciate any response.
It is possible to think about the point at infinity as the last point on the line, but then it’s also the first point on the line too! If you imagine the x-axis and go all the way to the right, there is a point at infinity at the very end there. But you can also get to the point at infinity if you go all the way to the LEFT too! The point at infinity on a line has to be at BOTH ends of the line simultaneously.
What this means is if you are travelling to the right on the x-axis and go past the point at infinity, then you COME BACK IN on the left hand side! In a way, when there’s a point at infinity, all our lines become sort of circular. So yes there are points “beyond” the point at infinity, but they are just the ordinary points that were behind you before.
Thank you for the clarification. So the lines marked for each w will then be akin to contours. When I get to w=0 contour, I’ll always find only line, so the line at infinity will not have the problem of being parallel to other lines at infinity, which in effect removes the “infinite'” recursion problem (for otherwise we will have to construct a line of infinity for the parallel lines of infinity to meet and the problem goes on ad nauseam).
So we can take w = 0 line as a mirror or a line of reflection whenever w is an even powered term in the homogenous equation. So we should expect both hyperbola and ellipses to have a reflection. In the case of hyperbola the reflection about w =0 complements the hyperbola we started with and the ellipse should be a reflection of itself. The reflection phenomenon takes us from the upper curve of hyperbola to the lower curve once we cross the line at infinity. So even in the case of a hyperbola, the ellipse we see is nothing but the hyperbolas jammed together about the line at infinity.
In the case of parabola, the reflection will give a complex number for one of the coordinates once we enter negative w values. Thus, the other half of the parabola is imaginary. So all we can see in our “real” world is only half of the parabola we started with.
Please correct this interpretation if wrong.
I’m not 100% sure what you mean by “contour” here. Are you seeing the equation as describing a set of points in 3D because it has three variables? That’s a most interesting way to view what is happening here. Note that all the quadratic equations here are homogeneous so that means that any 3D set described will be made of a collection of lines through the origin — essentially some sort of cone. In a way, what we usually see is the intersection of the plane w=1 with this cone.
The reflection thing is a rather interesting idea too. I like the idea that one branch of the hyperbola is a reflection of the other. Am I right in thinking you see one side of the line at infinity as representing w0? The problem with this is that every “real” point can be represented with either a positive w or a negative w as you choose. For example, the point (1,1,1) is the same as the point (-1,-1,-1). They both correspond to the real point (1,1). The point (1,1,1) is on your parabola yw=x^2, and so is the point (-1,-1,-1) which is actually the same point. We didn’t end up with a complex point after all when we use negative w’s.
Also, the line at infinity really only has one “side” — both the left side and the right side are the whole of the plane we see. All we’ve done by drawing the line at infinity as a line we can see is choose another line to be the line at infinity (for example, the x-axis is now drawn at infinity). So I think the reflection idea is really more of a metaphor than an exact description of what is happening.
PS: Did you read all the previous posts in the series, where I talk about what the w is all about?
Near the top of this page; it says:
… a point of the form (a,b,0) is the point at infinity belonging to all the lines parallel to ax – by = 0 …
From the latter part of the page it seems that (a,b,0) should go with x/a – y/b = 0
You are totally right. Good spotting. The point (a,b,0) is actually on the lines parallel to bx-ay=0. I’ve fixed the earlier comment now.
Bang on . Crisp. Cool. Real nature of conics exposed. Visualization of line at infinity. Projective geometry at its simplest . Big wow and big thanks.