This is the third in what has turned out to be a series on Where the Complex Points Are.
- Where the complex points are: introduction to the iplane concept
- Where the complex points are: on a line
- Where the complex points are: on a parabola (YOU ARE HERE)
- Where the complex points are: the graph of a function
- Where the complex points are: where the idea came from
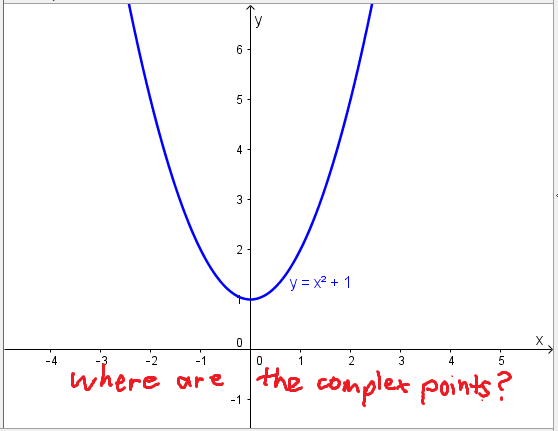
In the introduction, I talked about how I’ve always wondered where the complex points are on a parabola, especially wondering where the x-axis intercepts are if the parabola doesn’t meet the parabola.
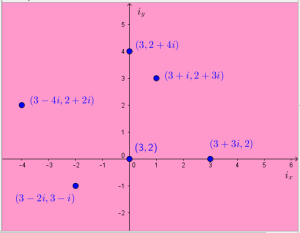
Then I described the place where I imagine the complex points are: at each point (a,b) in the real plane, there is an iplane attached, which contains all the points (a+ci,b+di). These points are arranged with the x-axis showing the imaginary part added to the x-coordinate and the y-axis showing the imaginary part added to the y-coordinate. I imagine them as being a transparent sheet attached to the point itself and being able to be flattened out to sit on top of the real plane.
In the second post, I talked about where the complex points are on a line. Now I’m finally ready to talk about where the complex points are on a parabola.
The points in each iplane
When I looked at lines with complex slope, I looked at each iplane individually and found out which points in that plane were part of the line. (There was one in each.) Let’s do the same for our parabola.
Consider a parabola with equation y = ax2 + bx + c and look at the complex points in the iplane attached to the point (p,q). That is, the points (p + ri, q + si)…
So we have an expression for r2. Since r is a real number, we’ll get a different number of solutions depending on whether this value is negative, zero or positive. But let’s look closer, when is this number negative, zero or positive?
Well, ap2 + bp + c is the y-coordinate of the point on the parabola with x-coordinate p.
So ap2 + bp + c – q is the vertical distance between the point (p,q) and the parabola. If the point is below the parabola, this value is positive; if it’s above the parabola, this value is negative; and if it’s on the parabola, this value is zero. The value of the coefficient a being positive or negative will change whether the whole expression is positive or negative. But it will also change whether the parabola itself is upward or downward curving. So overall we get the following possibilities.
| Point (p,q) below parabola | Point (p,q) on parabola | Point (p,q) above parabola | |
| Parabola upward-curving | Two solutions for r | One solution for r | No solutions for r |
| Parabola downward-curving | No solutions for r | One solution for r | Two solutions for r |
Since equation two only has one r, each solution for r will give one solution for s. This means that we now know many points of the parabola there are in each iplane, depending on where the iplane is attached.
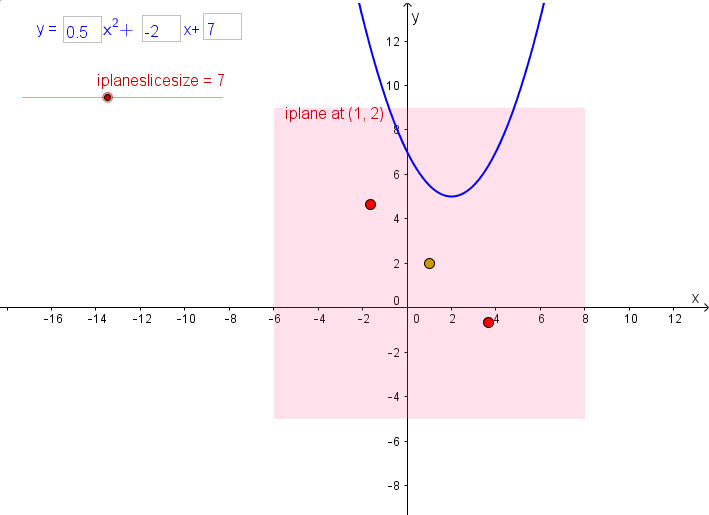
- If the iplane is attached to a point inside the curve of the parabola, then there are no points of the parabola in the iplane.
- If the iplane is attached to a point on the parabola, then this is the only point of the parabola in the iplane.
- If the iplane is attached to a point outside the curve of the parabola, then there are two points of the parabola in the iplane.
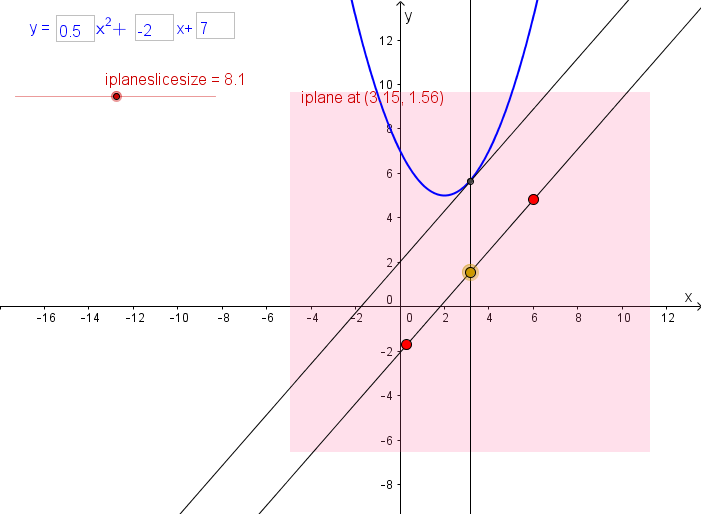
This GeoGebra applet allows you to investigate the complex points on a parabola in the iplanes attached nearby.
Collecting together iplane points
If you’ve played with that GeoGebra applet for a bit, you might have noticed that when you move the point where the iplane is attached, the complex points on the parabola move in interesting ways across the screen. It’s actually very interesting.
In a completely technical sense, the points we see in the iplanes in my GeoGebra applets aren’t really where they look like they are. They are up in iplane which only touches our real plane at the centre. It’s just that when we flatten a part of the iplane out and lay it on the real plane it’s easier to see the points. I’m going to make a new terminology to describe where the complex point looks like it is when you do this flattening out..,
Given a complex point, when the iplane it is in is flattened out to lay on top of the real plane, the real point where it appears to be is called the real image of the complex point. It’s quite straightforward to find the real image of a complex point directly from its coordinates: the complex point (p+ri,q+si) has real image (p+r,q+s).
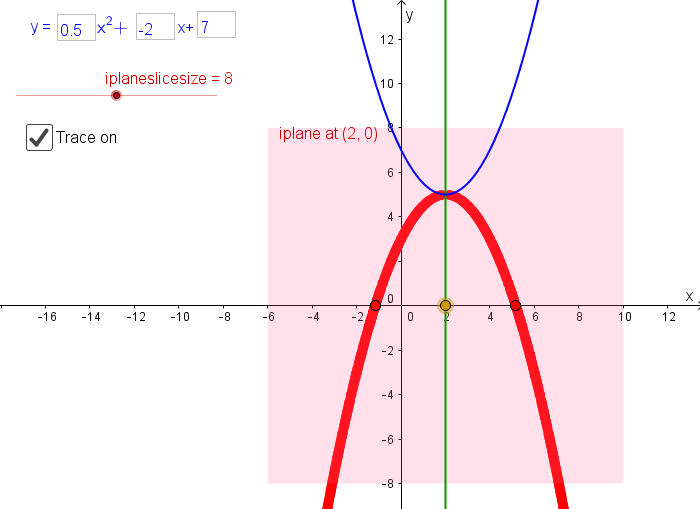
Anyway, what happens when you take all iplanes attached along a vertical line and collect together the real images of the parabola’s complex points in those iplanes? (There’s got to be a way to define terminology to make it easier to say what I just said! But right now I can’t think of anything good.) You can investigate this question visually in this GeoGebra applet.
Look at that! The real images of the points in the iplanes attached to that vertical line form a parabola of their own! The line I’ve shown there is the axis of symmetry of my parabola, and it appears that this parabola-of-real-images is just the original parabola flipped upside-down.
Let’s do some calculations. Think about all the points (x,y) that are the real images of the parabola’s complex points in the iplanes attached to the vertical real line x=p. These complex points are (p+ri,q+si) for some q, r, s and have real images (x,y)=(p+r,q+s).
So given any vertical line, if you look in all the iplanes attached to the line and collect together the images of the complex points in those iplanes, you make a parabola! What if the line is the axis of symmetry of the parabola? That is, what if p = -b/(2a)?
This is the equation of a parabola with vertex (p, ap2 + bp + c) — the same vertex as our original parabola. Its leading coefficient is -a — as opposed to +a for the original parabola — so it’s the same shape as the original parabola, but upside-down.
What this means is, if you want to find the complex points where a parabola meets, say, the x-axis, just flip it upside-down at the vertex and see where this parabola meets the x-axis. These are the real images of the complex points of the parabola on the x-axis, and they are in the iplane attached to the point where the axis of symmetry meets the x-axis.
iplanes and tangents
Did you notice the second equation we got above? It said that when (p+ri,q+si) is on the parabola then s = (2ap+b)r. The number 2ap+b is the slope of the tangent to the parabola at the point where x=p. The equation s = (2ap+b)r is an equation of a line of this slope inside the iplane through the centre of the iplane. When the iplane is laid flat on the real plane, you get a line of slope (2ap+b) through the point (p,q). This means that the complex points of the parabola in the iplane at (p,q) are both on a line parallel to the tangent to the parabola at the point where x=p.
But wait, there’s more! We just went vertically to the parabola from our iplane centre point. What happens when we go vertically to the parabola from those two complex points in our iplane? (Well, from their real images anyway.) The real image of these complex points are (p+r,q+s). The matching points on the parabola have x-coordinate x=p+r. Let’s find the y-coordinate:
Now q+s is the y-coordinate of the real image of our complex point, and we already figured out above that ar2 is the vertical distance from the point (p,q) to the parabola. So the y-coordinate is the y-coordinate of the real image of our complex point, plus twice the distance from the iplane centre to the parabola. That’s pretty cool. Even cooler is the fact that both complex points are the same vertical distance from their matching real parabola point, so the line joining these points is parallel to the line joining the complex points.
What this means is we now have a geometric way of finding the complex points on the parabola in the iplane at P=(p,q):
- Draw a vertical line from P to the parabola and mark the point on the parabola. Let’s call it A.
- Draw the tangent to the parabola at the point A.
- Copy the distance from A to P inside the parabola from A. Let’s call this new point B.
- Draw a line through B parallel to the tangent at A and mark where it meets the parabola. Let’s call these points C and D.
- Draw vertical lines through C and D.
- Draw a line through P parallel to the tangent at A. Mark where it meets the vertical lines through C and D.
These final two points are the real images of the complex points on the parabola in the iplane at P. You can see this construction in this GeoGebra applet. Isn’t that cool?
It also means we can do a similar construction to find where a particular line meets the parabola. Obviously if it meets the parabola in real points then there they are in the picutre. If it has no real points on the parabola, then we know that all the complex points on that line have real images on the line too. We also know that the complex points of the parabola in any iplane are on a line parallel to a tangent of the parabola. This means we have this geometric way of finding the complex points where a line meets a parabola:
- Find the tangent to the parabola parallel to your line. Mark the point where it meets the parabola A.
- Draw a vertical line through A. Mark the point where it meets the original line P — this is the centre of the iplane we need.
- Follow the construction above to find the complex points in the iplane at P.
If your line is a horizontal line, such as the x-axis, then this process is particularly simple because the only point with a horizontal tangent is the vertex.
Conclusion
So, in every iplane centred at a point outside the parabola there are two complex points on the parabola, and the real images of those points can be found via a geometric construction using tangents. Isn’t that totally awesome?
In the final post, I’ll talk about where this idea came from, because I think it’s totally worth mentioning.



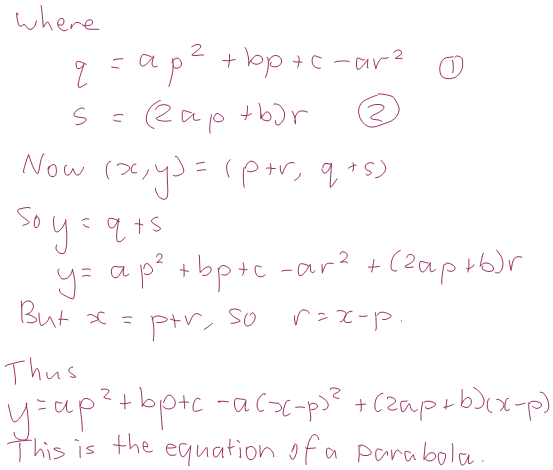
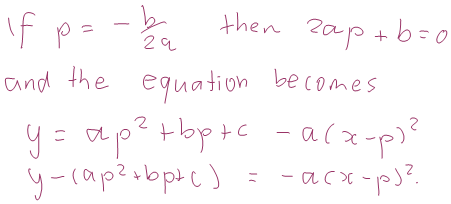


[…] Where the complex points are: on a parabola […]
[…] Where the complex points are: on a parabola […]