I have always loved the naming of quadrilaterals, right from when I first heard about it in high school. I’m not entirely sure why, but some of it has to do with the nested nature of the definitions – I like that a square is a kind of rectangle and a rectangle is a kind of parallelogram.
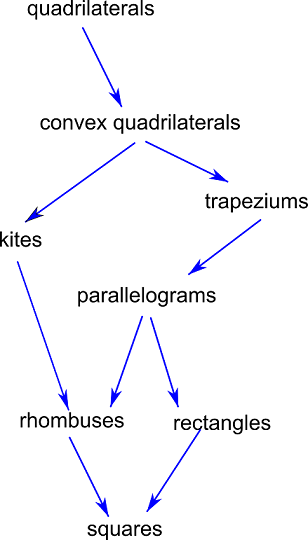
Most of the time you’ll see this classification organised in a sort of “family tree”. Like this:
(Warning: if you search for quadrilateral family tree in Google Images, you’ll get all sorts of things, many of which use American terminology, which is different to that here in Australia, and many others are just plain wrong.)
Of course, almost all people I meet are not aware of these nested definitions. Most students I work with are bamboozled when the answer to the problem of the largest area rectangular garden of fixed perimeter gives them a square. To them, a square is not a rectangle. Then again, there are others who aren’t aware that orientation is not one of the factors mathematicians use to name shapes. Just the other day someone asked me why a shape was called a diamond if it’s this way and a parallelogram if it’s this way. (That was a most interesting conversation about language and maths and maths language.)
Partly I think this is because the only examples we give of rectangles are non-squares — we never include squares in a collection of rectangles. Also, almost all examples we give of these things have their edges parallel to the top and bottom of the page. The casual viewer comes to believe that the orientation is part of the defining properties. A serious case of Beware of the Toast.
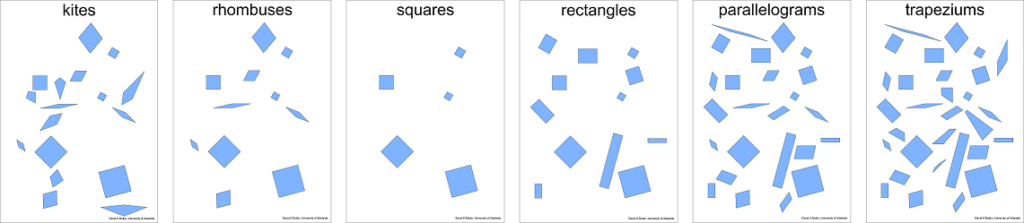
For a long time, I’ve wanted to make some posters showing collections of quadrilaterals including ones not parallel to the page edges and including the more special ones further down the tree. And yesterday I just decided that I would finally do it.
Here’s a picture of the majority of them. (You can find them in pdf form here.)
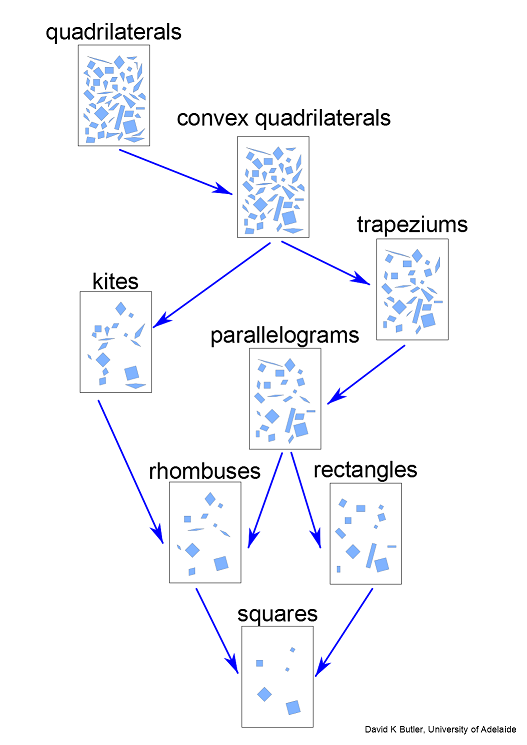
And finally, an upgraded family tree, showing heaps of examples of each type of quadrilateral. (You can find this in pdf form here.)
PS: If you want the original svg files in case you want to edit them (for example, to make them into local terminology), just ask.

Hi David
Many thanks for putting together and sharing the Quadrilateral Family Tree. I plan to share it with the classes I teach.
Anne Kelly
Geographe Primary
WA