Last week, I helped quite a few students from International Financial Institutions and Markets with their annuity calculations, which involve quite detailed stuff like this:
There were several small issues a lot of them had, which combined to stall their calculations. One of the more important problems was about how the calculator interprets what they type into it, which is really in essence about the order of operations.
When I look at the formula above, I see many pieces that are put together in various ways to make a number called “PV”. These pieces are combined using various operations, and are also held together in order to go into these operations with various grouping symbols. Some of these things have a stronger “hold” than others and will enforce certain things to be done before other things are done if I were to actually do this calculation. This is the “order of operations”. I’ve written about it before, but I’ve moved on in my thinking quite a bit since then!
While many people use some sort of acronym to remember the order of operations, that has never worked for me. Instead I have a picture of a hierarchy of operations like this:
When I draw this on paper, I start at the bottom, drawing the + and – first. Then I draw the × and ÷ above that. Then I draw the ^ and √ above that. Finally I draw the box on the side with the (), [], ___. The idea is that + and – are the most basic and hence least important to do before things nearby followed by × and ÷ and then by ^ and √ . The symbols on the side are for holding things together in order to override this hierarchy. It’s worth noting that I use this picture to remind myself which things expand out over which things when there’s brackets in the way. (If I was particularly clear-minded, I might draw the × and + even further to the left than the others because they work fine in both directions whereas everything else is different in different directions.)
Anyway, this order of operations allows me to analyse the expression above and tells me that the r/n on the bottom there is held together before it becomes part of the larger division. It tells me that the r/n inside the brackets is more important to calculate before the “1+”. I also know, though it’s not written in my order of operatons picture, that the little -nt is all inside the top of that power, and needs to be done before I can resolve the power itself.
Unfortunately, the scientific calculator (or Excel, or Wolfram Alpha) is less clever than this. When I type things into the calculator, it can’t see the physical arrangement of things on the page. It can’t tell that some things are smaller than others and arranged at the top. It can’t see that there’s a big horizontal line holding the r/n together. The only way the calculator knows to hold things together is with some brackets. So I’m going to have to turn all the things that visually hold things together into brackets.
So suppose I wanted to calculate the following:
If I only typed the symbols I see like this:
1000÷0.06÷12×(1-(1+0.06÷12)^-12×30)
Then I would not get the result I hoped for. The calculator would certainly do the 0.06÷12 inside the brackets before the “1+”, but it will do the 1000÷0.06 before the “÷12” at the front, and it will do the “^-12” before the “×30” too. I have to tell the calculator explicitly what to hold together using brackets. Like this:
1000÷(0.06÷12)×(1-(1+0.06÷12)^(-12×30))
I find this sort of discussion very important and very helpful for the student. It’s so important to help them see what is held together by the brackets and by the horizontal lines and the powers. And it’s also so important to help them see that the calculator is like they were a few minutes ago — it can’t tell that those things hold other things together and just needs to be told every time.

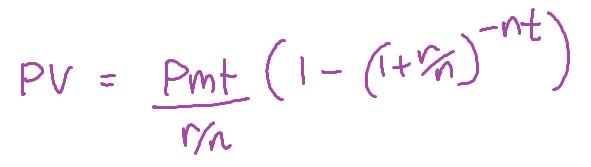
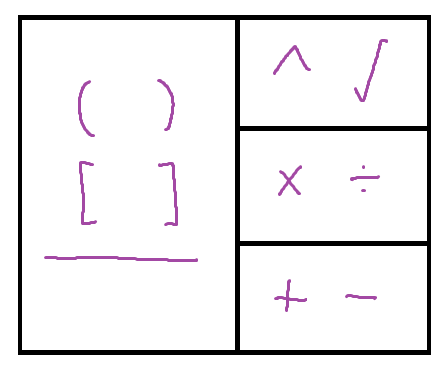
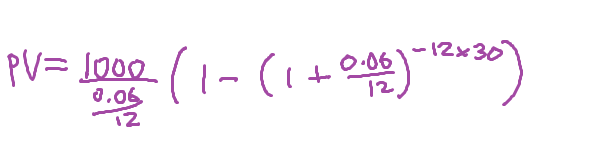
I teach this skill, too, in my Algebra 1 classes. I sometimes wonder whether better computer/calculator interfaces will eliminate the need for this skill in a couple years. For example, I make a big deal out of the fact that, to square 3/5, you need to type (3/5) with parentheses. But that’s actually not true in the newer graphing calculators.
I don’t think we’ll eliminate this skill in its entirety for quite a long time! Firstly, there will be for quite some time yet, interfaces that are more computer-programmy (like Excel and the fancy statistics manipulation software). Secondly, this discussion often highlights they don’t actually know what the powers or fraction bars are doing anyway. Something that is able to copy their writing and interpret it might mask that misunderstanding!