I was talking to a student about his calculus last week. He was trying to differentiate xx. (Actually he was trying to differentiate x ln(x) and had decided the best place to start was to raise e to the power of it, thus producing xx.) At first he tried this:
I asked him what he thought about that and he said he wasn’t sure it was right because of the x in the power. I asked him how you normally dealt with an x in the power. He thought about it and then produced this:
I confirmed that this is indeed what you would do if there was an x in the power but the base was constant. But I also confirmed that because there was an x in both the power and the base, it was going to be a bit trickier. He asked how you did deal with that, and I started out by writing xx = (eln(x))x. (On reflection, if I was doing SQWIGLES properly, I should have helped him find this definition in his notes.) Together we continued this working as follows. Interestingly, we ended up having to differentiate x ln(x) as part of this, but by this time he realised it would be much simpler to use the product rule!
Do you notice anything interesting about that result? Well, I did: it’s the sum of the other two wrong answers! If we treat the base as a constant we get a (wrong) result, and if we treat the power as a constant we get a (wrong) result, but if we add those two results together we get the correct result! This is WILD!
After we did the summing up what we’ve learned bit, I absolutely had to try this out generally to see what would happen (you can read this working in a pdf here):
Oh my goodness! It worked again! I am reeling with the wildness of this! Currently I don’t know if there’s a more conceptual/visual approach to this that will help me feel like I understand why it is true, but for now I’m just going to relish the wildness of these two wrong results adding up to the correct one.
PS: Isn’t it cool the stuff you learn when you listen to students? If I’d just told him what to do I’d never have noticed this.

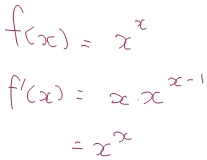
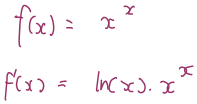
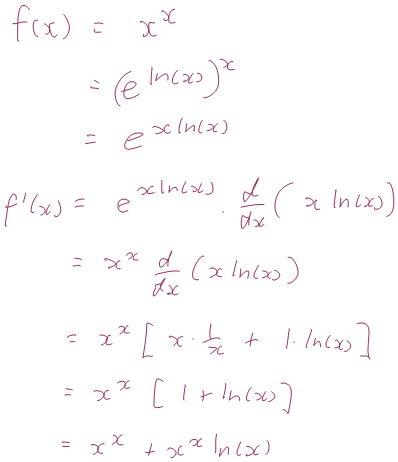

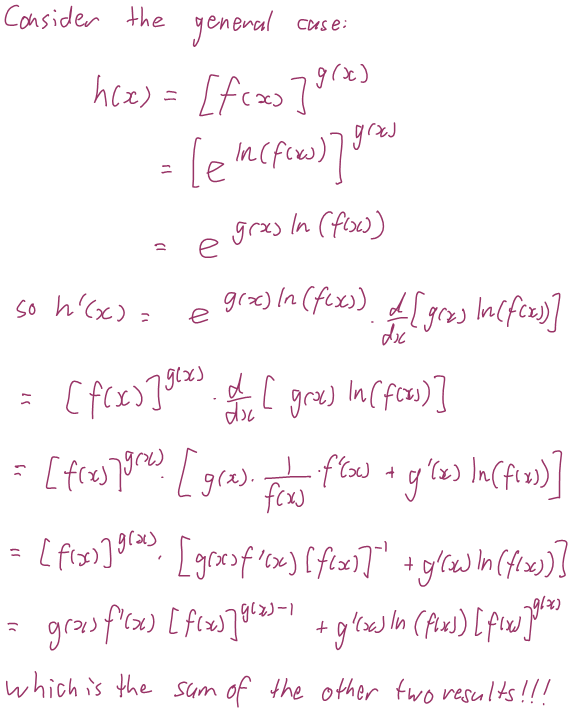
This can be explained using the multivariable chain rule. Let f(u,v) = u^v, u=x, v=x. Then df/dx = ∂f/∂u du/dx + ∂f/∂v dv/dx = ∂f/∂u + ∂f/∂v. The product rule is also a special case of the multivariable chain rule.
Ah you beat me to it! I was just going to do an update to say exactly this!
In my head it was something like f=u^v with u=f(x) and v=g(x).
So df/dx = df/du*du/dx + df/dv*dv/dx
= (derivative of f treating v as constant) + (derivative of f treating u as constant)
Of course, this student won’t see multivariable calculus in their course for another several months yet…
[…] seems like ages ago — but it was only yesterday — that I wrote about differentiating functions with the variable in both the base and the power. Back there, I had learned that the derivative of a function like f(x)g(x) is the sum of the […]