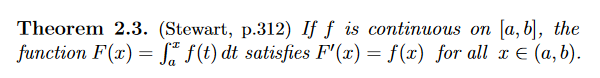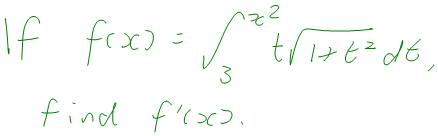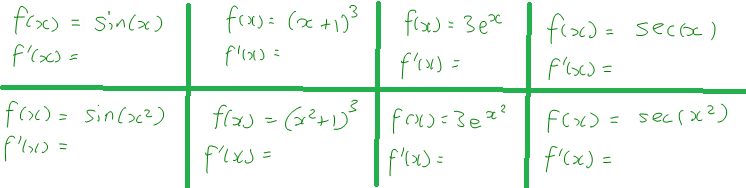In Maths 1A here at the University of Adelaide, they learn the following theorem (this is taken from the lecture notes written by the School of Maths here):
It says that, given a function of x defined as the integral of an original function from a constant to x, when you differentiate it you get the original function back again. In short, differentiation undoes integration. In many places in the world, including in the textbook for this course, this theorem is called “Part I of the Fundamental Theorem of Calculus”. (Part II says that integration can be done by doing differentiation backwards. Here at Uni of Adelaide, only Part II is called the Fundamental Theorem of Calculus. Go figure.)
And then they get questions something like this on their assignments and they don’t know what to do. They always say something like “I would know what to do if that was an x, but it’s not just an x, so I don’t know what to do”.
I have a way of thinking about this that makes sense to me and it has to do with blocking what I see into blobs and a mantra I say to myself when I am faced with certain derivatives (I will probably write about that soon). However, I know that this doesn’t always make sense to students when I tell it to them for the first time. When I was with a student grappling with this last week, I suddenly realised that I had come to my own way of thinking because I had noticed a pattern in the way derivatives worked and noticed that I could apply my pattern to this situation. So I decided to take a different approach and help the student notice this pattern for themselves.
And what do you do to make a pattern more obvious? You line things up!
I made a grid and said to the student I would write problems in the grid for him to do, and to bear with me because I did have a point I promise. So for the next several minutes I wrote a new problem in the grid and passed it over for him to do it, asked him what his thinking was in that problem, and then wrote another one for him to do, and so on. I was very proud of myself for relinquishing the pencil and letting him do all the writing – this is the part of SQWIGLES I often find the hardest.
These were the problems we did, approximately (it was almost a whole week ago now). I was particularly proud I thought of f(x) = sec(x), because its derivative has two x’s in it:
At the end I asked him what he noticed about the problems and if anything he noticed would help him with the one at hand. And he figured it out! He noticed that all of them had an x in one version and an x2 in the second version, and he noticed that in every one, you did exactly the same move on the bottom row as the top, but multiplied by 2x each time. And he straight away wrote down the correct result for his problem with the derivative of an integral and articulated a general rule he could use in the future.
I couldn’t have been prouder of him. Internally, I couldn’t have been prouder of myself for using this approach. I am led to believe that this sort of thing is called a “problem string”, and I want to notice more opportunities to use them because I have a feeling it will be way more empowering for students. I’ll certainly use problems strings next time I am called upon to help a student understand using the chain rule when a function is defined as an integral!