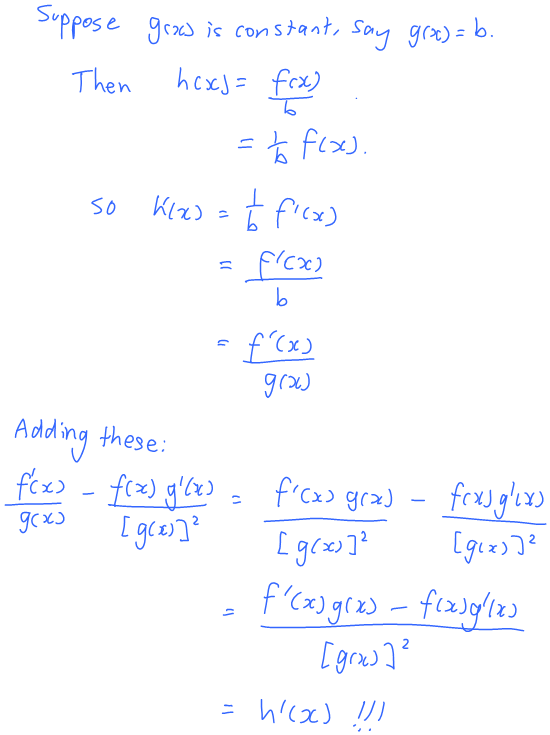It seems like ages ago — but it was only yesterday — that I wrote about differentiating functions with the variable in both the base and the power. Back there, I had learned that the derivative of a function like f(x)^g(x) is the sum of the derivative when you pretend f(x) is constant and the derivative when you pretend g(x) is constant.

Since then I have realised that this idea actually dictates ALL of the differentiation rules where two functions are combined through an arithmetic operation! It’s everywhere! Look:

Multiplication…

Oh my goodness – it’s the product rule!

Division…

Oh my GOODNESS – it’s the quotient rule!

Addition…

OH MY GOODNESS – it’s the addition rule!

So it’s everywhere! This is totally awesome!!

In the comments in the last post, it was mentioned that the reason all this happens is because of the multivariable chain rule, which is all about holding all but one variable constant and adding together the different results. When I realised this I thought to myself “duh!” – I was using the same words to tell myself what to do in both situations.

The issue is that when students learn these rules, they don’t know multivariable calculus so this can’t be used as a way to explain what’s happening. But I have a good feeling that it might be able to help make sense of the multivariable chain rule when they do learn it because it will connect perfectly so something they already know. I’ll let you know if I ever try.