There is a Twitter account that tweets the prime numbers once an hour in sequence. (The handle is @_primes_.) Since before I joined Twitter, it’s been working its way through the six-digit primes and some of them are very nice. A lot of other people think they’re nice too, based on the fact that they are given likes and retweets. But what is it that motivates people to do this? What is it that makes a prime likeable? Well, that’s what this post is about.
I was planning to do this investigation over Summer, and at the time I got Lewis and Tobin to help me get the data on the prime tweets over the previous few months. Tobin did some analysis of his own, but I haven’t looked closely at it because I wanted to have the fun of doing it myself. Not until now have I had the chance to actually do it. So here goes! What you see here is a record of my thoughts and investigations as I did them.
I have data on primes tweeted between the 11th September 2016 to 26th January 2017, a total of 3217 tweets. I think there’s a gap of time in there with no data, but for our purposes it should be enough. You can get the raw data here: likeable-primes-data.csv
First up I’ll just have a look at how many likes each prime has gotten and see what we might see.
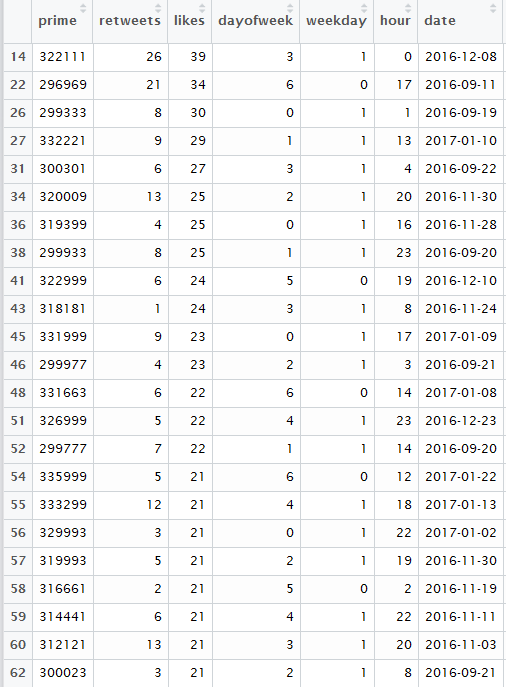
Oh my! Well one prime in particular is way more likeable than all of the others, and there’s a couple more there that are quite a lot higher, but not nearly in the same league. Let’s have a look at the top ten and see what they are.
Well would you look at that top one?! It’s the first several digits of pi. So it seems that the most likeable thing about a prime is being pi. It seems you have to be right on the dot though – being close just isn’t all that likeable as this list of primes starting in 3141 shows:

I could try to search to see if being the digits of other special numbers is likeable, but it seems the digits of other special numbers just aren’t prime. Pi itself was last prime at 31, which doesn’t stand out as pi-ish, and it’s not going to be prime again for quite some time. Phi and e aren’t going to be prime until seven digits, and the square root of 2 won’t be prime until after 50 digits, so it’s going to be a while before I can check the effect of this on prime likeability. (Check out pi-prime, e-prime, phi-prime and this wolfram alpha search.)
I wonder what it is that made those other highly likeable primes have so much love? I see in the top ten list a whole lot of primes with lots of the same digit, so it seems repeated digits is something highly likeable.
I might come back to that later because I also see 300007 and 299993, which are the first primes before and after 300000. Maybe there’s also something in primes being close to milestones. I’m not sure if there’s any other good milestones in this range of primes to test this theory. Let me go searching for the prime tweets near to other milestones…
Aha! Just a couple of weeks ago we reached the 400000 milestone and there was a spike in likes before and after. There were also spikes when 200000 was passed in 2015 and when 100000 was passed in 2014. So yes it does seem that primes before or after milestones are liked more. It’s interesting that 199999 got so many more likes than 200003. I’m wondering if it’s to do with the repeated digits thing that I mentioned earlier.
So what about these repeated digits then? It seems primes with a lot of repeated digits get more likes. There’s a lot of factors there that might be at play – is repeated digits in a row more likeable than separated? How many repeated digits do you need to get more likes? So many questions!
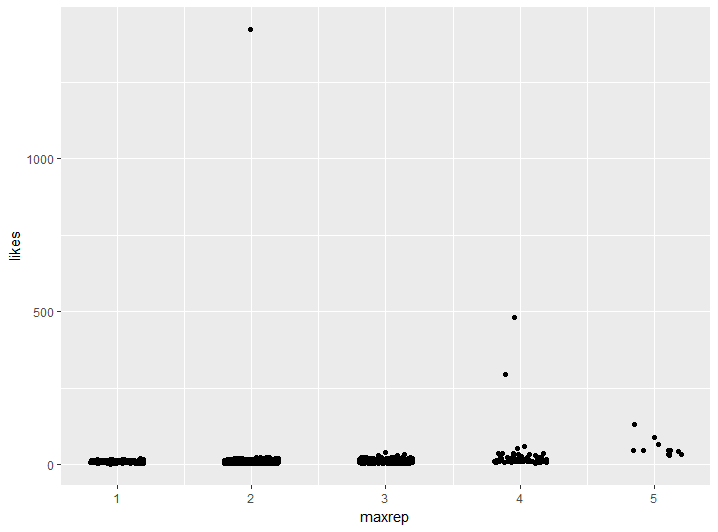
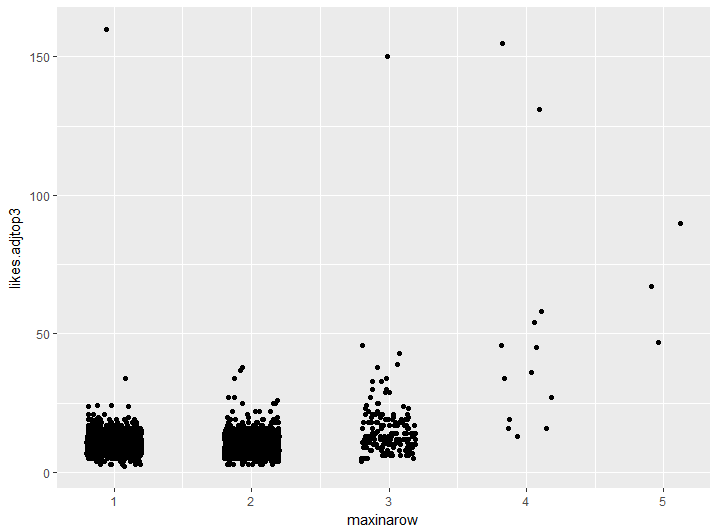
Well first I’ll count how many of each digit there are in every prime, and I’ll find the maximum number of repeated digits. I’m not looking at repeated digits in a row right now. I’m not sure how to do that yet. Let’s look at the relationship between highest number of repeated digits and likeability.
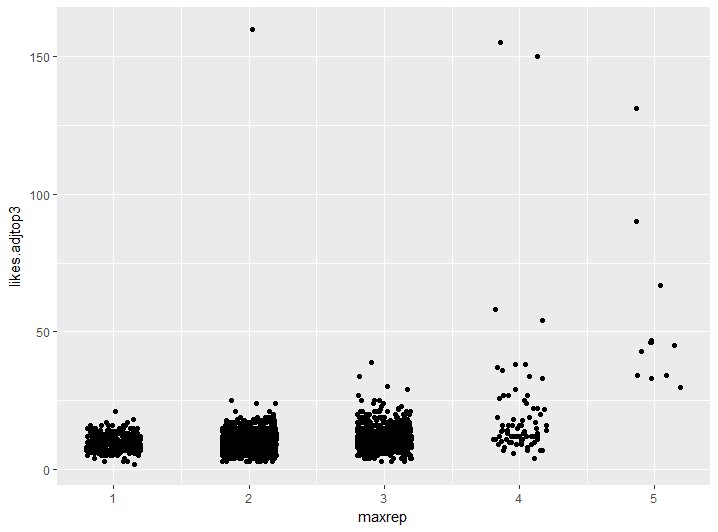
Oops! That 314159 is making it hard to see what’s going on here! Those other two really big ones could make it hard to see too. I could remove those top three, but I don’t want to lose the fact that they are there. What I’ll do is replace them with something just above the next one down, like 150, 155 and 160. Let’see if I can get a better look at what’s going on down the bottom there after that.
This is much better — there’s definitely something going on there. Primes with five repeated digits are certainly more likeable than primes with less, and four repeated digits definitely seems to increase the chances of likeability.
My attention is drawn to those few extra-likeable ones leaping out of the clump of primes with digits repeated three times. I want to look closer at those.
Some of those are rather nice, but there’s nothing I can see that they share which makes them particularly likeable. Let me widen the search to include the next few most likeable.
Ah! I see most of these have their triple digits all in a row as opposed to separated. A lot of them also have a double-digit too. Other than that, I can see ones with an alternating pattern. Those are going to take a bit of learning for me to figure out how to find them…
Phew! That was some hard work! And unfortunately it doesn’t really tell me anything that much different than the number of repeated digits ignoring the number in a row.
Let’s look at them together: in the graph red is “in a row” and blue is “repeated at all”. If a prime already has repeated digits then having several in a row might make it a little more likeable, but I don’t know if it was worth all the effort to figure out how to get R to count them. The graph is pretty though.
I’m not sure I want to figure out how to search for an alternating pattern. Someone I’m sure will say “just use regular expressions” and I would say in response that I don’t know how to use regular expressions and I’m not sure I care to learn right now. Plus I suspect it probably doesn’t add much more to the likeability compared to just having repeated digits in any order.
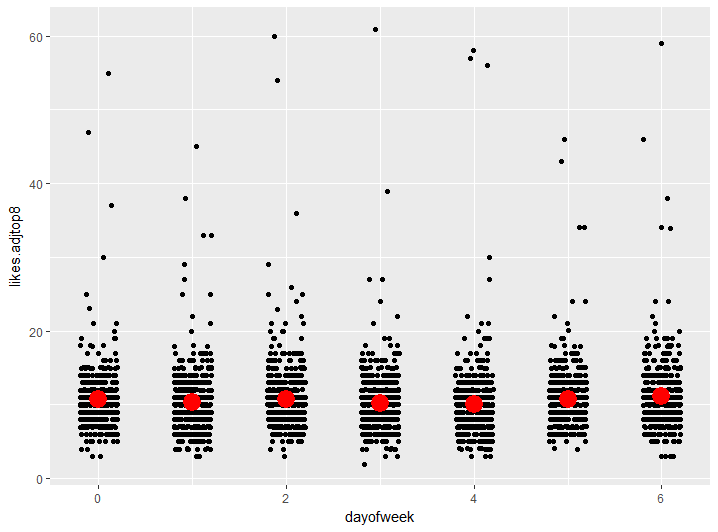
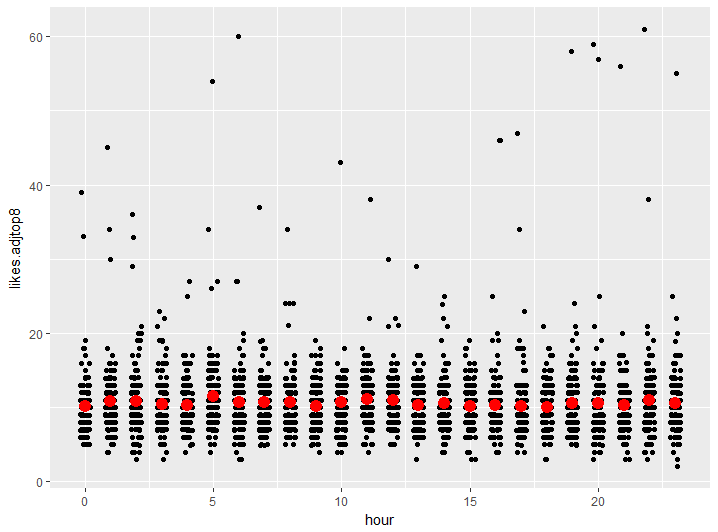
Well that pretty much exhausts the things I noticed looking at the most likeable primes. The first thing anyone has suggested when I have mentioned I was doing this was that perhaps time when it was tweeted has an effect, so I might as well take a look. I think the primes with above 50 likes can be attributed mainly to repeated digits and piness, so I’ll just adjust those like I did before. These graphs show the likes on days of the week or time of day, with the mean marked by a red dot.
There’s variation between days/times certainly, but I don’t see that it makes all that much difference to the number of likes compared to the total amount of variation. Actually, my stats-ear is saying I should back that up with some tests. These ANOVAs say that the day of week or time of day don’t really make much of a difference compared to the rest of the variation.
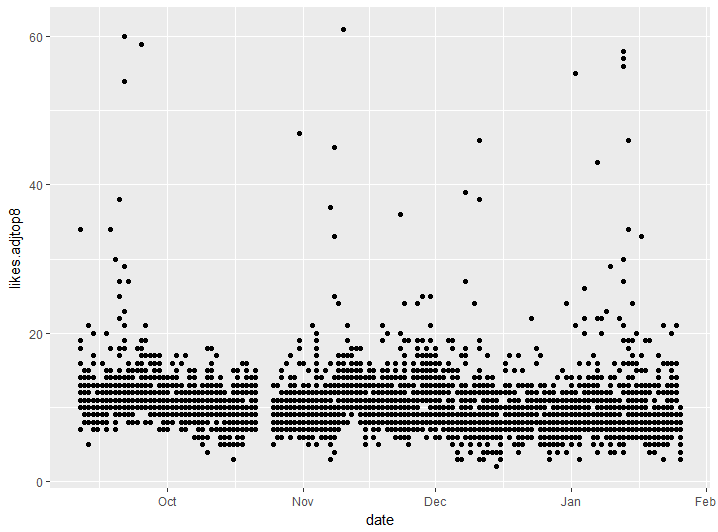
I suppose I could look at the grander sweep of time to see if there’s anything interesting going on there.
Well first I notice a gap in October. Now that I see it I think I do remember Tobin saying something about some missing data. I also notice that in October there aren’t many primes with a lot of likes. I’m not sure what caused that. I do know that most of those highly-liked primes are repeated digits, so what if I colour by the maximum number of repeated digits to see how that relates?
Wow! It seems that almost all of those primes above the river are ones with 4 or 5 repeated digits, and there just happen not to be many of them in October. I can see a few orange dots in the mix there and I do wonder why those ones aren’t very likeable. Interestingly, there’s a lot of orange dots down the bottom there in January. But there’s also a lot of yellow there which means three repeated digits. Maybe in comparison to the general repetition of digits at the time, they just didn’t seem as special as they did back in November when there had been a repeated-digits drought. (Upon closer investigation, that January period is when we were passing through the 330000’s so we were guaranteed to get double 3’s for a while.)
I also notice that there is an upward bend in the river around 314159 in early November and the milestone of 300000 in late September. I think perhaps the twitter account generates higher levels of attention around an important event, which means that likes are more likely. This might explain the high number of likes for 301333, even though it only has three repeated digits a row: it’s the first prime after 300000 with three nonzero repeated digits in a row, so it got more attention because of the afterglow of the milestone.
The final thing to consider is if there is anything that makes a prime specially unlikeable. Let’s have a look at the bottom twenty or so.
I can’t see anything in particular that sets these ones apart, which I is the point I suppose! I do feel sorry for poor 324619, which has the dubious honour of being the least-liked prime in this timeframe. (And as a result, it’s no longer the least-liked prime in that timeframe. )
324619
— Prime Numbers (@_primes_) December 15, 2016
I suppose it’s time to sum up. What have I found out here?
The following things seem to make a prime number more likeable:
- Being pi
- Being close to a milestone
- Having a lot of repeated digits, especially if not near other primes with repeated digits
- Being near pi or a milestone
Well. That was fun!




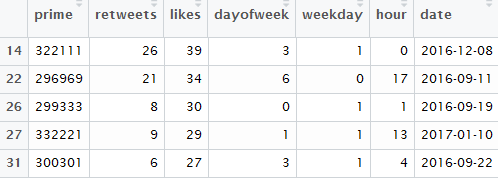



[…] he’s done some wonderful research on likeable primes! This is a great article with some fun conclusions! Before you read it, take a guess for yourself […]