Introduction
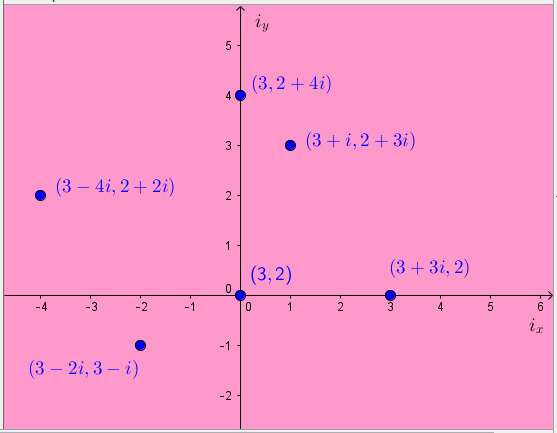
In 2016 I created the iplane idea, which allows you to locate the complex points on a real graph.
In case you haven’t heard of it or you need reminding, the idea is that at every real point (p,q) of the real plane, there is a planes-worth of complex points attached, all of which have coordinates (p+si, q+ti). The collection of all the points with real part (p,q) I called the iplane at (p,q), and I imagined the iplane as a transparent sheet attached at the point (p,q) which I could flatten out to see its points when I needed to.
Ever since I had this idea, I have wondered on and off about the complex points on a circle. It’s time to write about what I’ve found.
In this blog post, I will investigate the complex points on a real circle centred at the the origin. (In later blog posts, I’ll think about “unreal” circles, but you may need to wait a while for those.)
Investigating complex points on a real circle
I’ll consider the circle with equation x²+y² = r², where r is a real number with r>0, and I’ll try to find the complex points on this circle in the iplane attached at the real point (p,q).
The points in this iplane have coordinates (p+si,q+ti) for real numbers s and t. If such a point is on the circle I’m considering, then it would have to satisfy the equation. So I’ll sub it in:
(p+si)² + (q+ti)² = r²
p² + 2psi + s²i²+q² + 2qti + t²i² = r²
p² + 2psi – s²+q² + 2qti – t² = r²
The number on the left is the same number as the number on the right, so their real and imaginary parts will be the same.
Real parts:
p² – s² + q² – t² = r²
p² + q² – r² = s² + t²
s² + t² = p² + q² – r² (Equation 1)
Imaginary parts:
2ps + 2qt = 0
ps + qt = 0 (Equation 2)
These equations together describe the (s,t) coordinates of the points in the iplane at (p,q) that are on the circle. Let me investigate them separately.
Equation 1 has real solutions for s and t — and they have to be real because s and t are real numbers — when
p² + q² – r² ≥ 0
p² + q² ≥ r²
√(p² + q²) ≥ r
Now √(p² + q²) is the distance of the point (p,q) from the origin, so there are solutions for s and t in Equation 1 when the point (p,q) is at least r from the origin. That is, when (p,q) is on our OUTSIDE the circle!
Just to be absolutely sure, let me just check.
When (p,q) is inside the real circle, then
p² + q² < r².
So p² + q² – r² is negative, which means that
s² + t² = p² + q² – r² has no solutions.
So there are no points of the circle in the iplane at (p,q) if (p,q) is inside the real circle.
When (p,q) is on the real circle, then
p² + q² = r².
So p² + q² – r² =0, which means that
s² + t² =0,
And that means s=0 and t=0.
This also satisfies Equation 2 since p*0 + q*0 =0.
So the only pair (s,t) that satisfies both equations is (0,0), which corresponds to the centre of the iplane at (p,q).
That is, when (p,q) is on the real circle, then the only point of the circle in the iplane at (p,q) is (p,q) itself.
Ok, so I can now get back to the iplanes at the points outside the circle.
Let (p,q) be a point outside the circle, which means p² + q² > r² and so p² + q² – r² is positive.
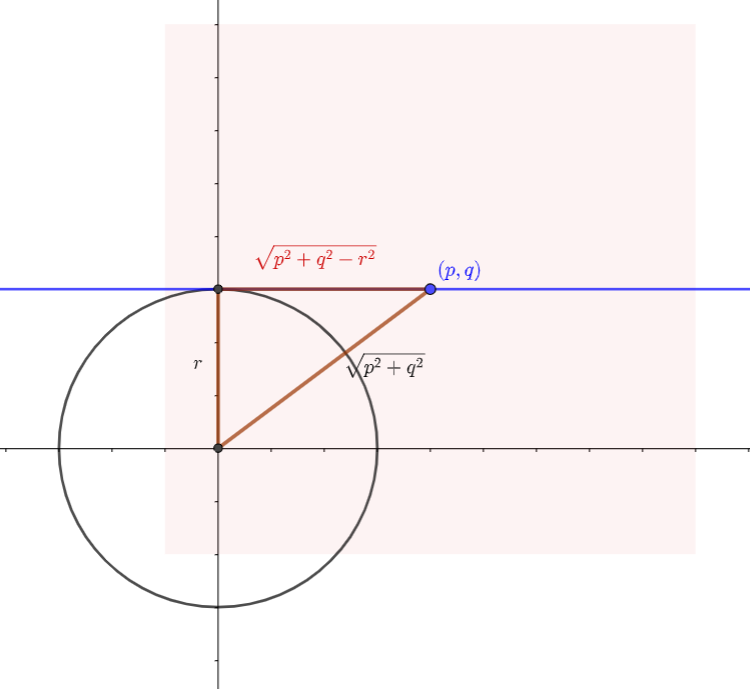
Therefore s² + t² = p² + q² – r² is the equation of a circle (inside the iplane at (p,q)), centred at (p,q) and with radius √(p² + q² – r²).
That radius √(p² + q² – r²) ought to be a short side in a right-angled triangle with hypotenuse √(p² + q²) and other short side r.
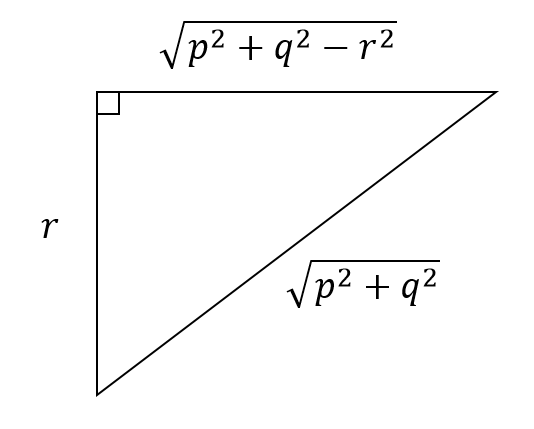 But I know those distances! The distance √(p² + q²) is how far (p,q) is from the origin, and the distance r is the radius of the real circle. If the distance √(p² + q² – r²) meets a radius in a right angle, then that means it’s a tangent to the circle! So that means I am looking for the distance along a tangent drawn from the point (p,q) to the real circle! Of course, this construction is happening inside the iplane, as it is lying flat on top of the real plane so I can see the real circle through it.
But I know those distances! The distance √(p² + q²) is how far (p,q) is from the origin, and the distance r is the radius of the real circle. If the distance √(p² + q² – r²) meets a radius in a right angle, then that means it’s a tangent to the circle! So that means I am looking for the distance along a tangent drawn from the point (p,q) to the real circle! Of course, this construction is happening inside the iplane, as it is lying flat on top of the real plane so I can see the real circle through it.
The points I am looking for are on a circle of radius √(p² + q² – r²) drawn inside the iplane centred at (p,q). But this is only based on Equation 1. The complex points on the original circle in the iplane also satisfy Equation 2:
ps + qt = 0
(p,q) · (s,t) = 0
So the vector (s,t) is perpendicular to the vector (p,q). The vector (s,t) is the vector from the centre of the iplane to the point (s,t) inside the iplane, while the vector (p,q) is the vector from the origin to (p,q). So the line ps+qt=0 inside the iplane passes through the centre of the iplane at (p,q) and is perpendicular to the line from the origin to (p,q). Which means the points I am looking for can be constructed like this.
To find the points of the circle with equation x² + y² = r² in the iplane at a point (p,q) outside the circle:
- Lay the iplane at (p,q) flat over the real plane.
- Draw a tangent from (p,q) to the real circle.
- Find where this tangent meets the circle, then draw a circle inside the iplane through this point, centred at (p,q).
- Draw a line perpendicular to the vector (p,q) inside the iplane at (p,q).
- Find where this line inside the iplane meets the circle inside the iplane.
- These two points are the points of the original circle inside the iplane.
This GeoGebra graph allows you to see the complex points on a real circle in the iplane at a moving point (p,q). You can turn on and off the construction lines used to find the points.
I feel like I need to do one final thing: to find the actual coordinates of those points, which means formally solving those equations.
s² + t² = p² + q² – r² (Equation 1)
ps + qt = 0 (Equation 2)
From Equation 2:
ps = -qt
p² s² = q² t²
Multiply both parts of Equation 1 by p²:
p²s² + p²t² = p²(p² + q² – r²)
Substituting the result of Equation 2 into this:
q²t² + p²t² = p²(p² + q² – r²)
(q² + p²)t² = p²(p² + q² – r²)
t² = p²(1 – r²/(p² + q²))
t = ±p√(1 – r²/((p² + q²))
From Equation 2:
ps = -qt
s = q/p t
So if t = p√(1 – r²/(p² + q²)), then s = -q√(1 – r²/(p² + q²))
and if t = -p√(1 – r²/(p² + q²)), then s = q√(1 – r²/(p² + q²)).
Technically, this argument doesn’t work if p=0, but then a similar argument using q instead will produce the same result. (And it doesn’t matter if they’re both zero because I already know there are no solutions then anyway.)
So, the points of the circle with equation x²+y²=r² in the iplane at (p,q) are
(p-q√(1 – r²/(p² + q²))i,q+p√(1 – r²/(p² + q²))i )
and
(p+q√(1 – r²/(p² + q²))i,q-p√(1 – r²/(p² + q²))i ).
(Note how these are the same point when √(p² + q²) = r and they are undefined when √(p² + q²) < r.)
A new representation
The fact that the two points on the circle in the iplane at (p,q) are both on a circle centred at (p,q) tells me they are the same distance inside the iplane from the centre.
Thinking all the way back to my physical model, the iplanes can be folded up like umbrellas, like this picture but in reverse:
If I do that, then every point inside them would end up on a vertical line, at a height equal to the distance away from the centre point. That seems to me like a very nice representation! In this case it’s particuarly convenient because both points are the same distance from the centre of the iplane, and so the same height.
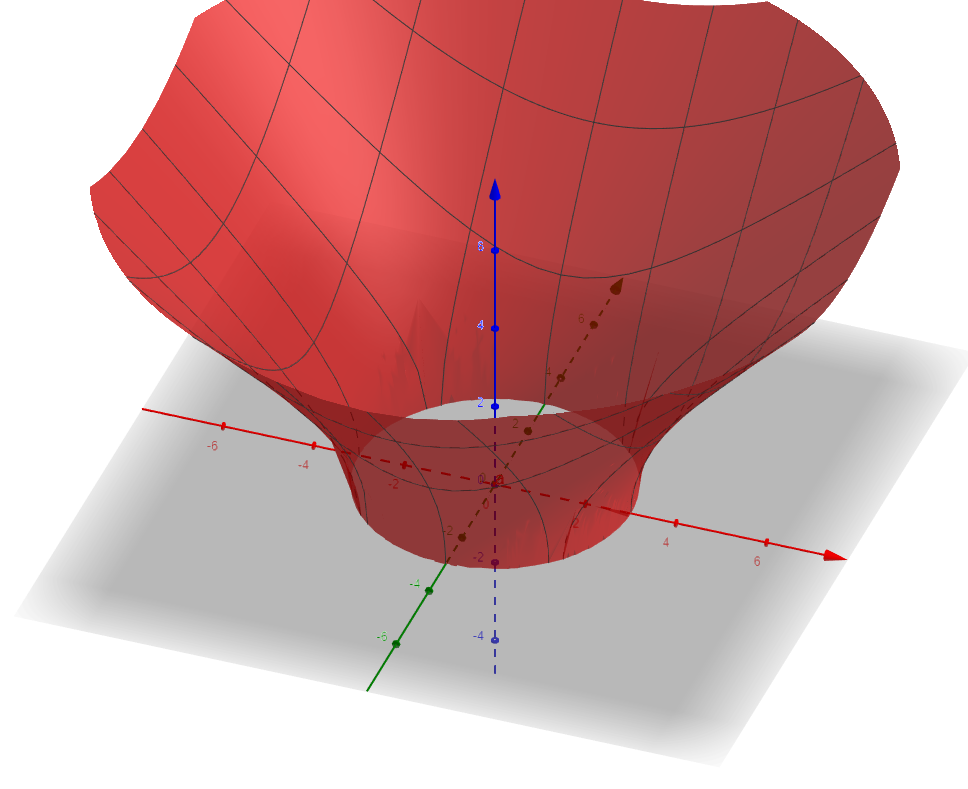
For our circle x²+y²=r², the points on the circle in the iplane at (p,q) are a distance √(p² + q² – r²) from the centre of the iplane, so my “folded umbrella” representation will have a point at height z =√(p² + q² – r²) at each point (p,q) and it will come out like this:
You can see an interactive version of this graph which you can drag around to look at from different perspectives here: interactive folded umbrella iplane graph.
One thing I love about this graph is the sense that some complex points are closer to being real than others. In the graph, you can see there are no points of the circle (real or otherwise) inside the circle, and as you move further away from the real circle, the complex points get further and further from being real. The points on the circle far away from the real circle are very far from being real, which appeals to me.
(Of course, if I had two such graphs, there would be no guarantee that the places where they met would actually indicate shared complex points, because every height can be created by anything in the iplane on a circle of that radius. But still useful for thinking about one graph.)
Where next
I am going to have to investigate the folded umbrella representation of the complex points on an object more at some point. I really want to see how it looks for the complex lines and parabolas I already investigated four years ago. But first I would like to investigate what happens for an unreal circle. What does the circle look like when it has x²+y²= R for some negative number R. In a sense, that would be a circle with negative area. And what if the area was any complex number? But those are other stories and shall be told at another time.