BLOGS WEBSITE

UPDATES on the complex points on a line using i-arrows

Posted on July 26, 2022 by David Butler

On 27th July 2022, I wrote a blog post about using i-arrows to make sense of the complex points on both real and unreal lines. And at the end I mentioned how there were still some things mysterious to me. But of course I kept thinking about them and now I know more things.

I’ll keep posting updates here in this blog post as long as I have them, or until I have to stop and do other stuff.

UPDATE  1 (about 9:30pm 26/7/2022)

I have at least been able to prove the that the further the base of your i-arrow is from the real point on an line of unreal slope, the longer the arrow is. Here goes…

Suppose Ax + By = C is the equation of a line of unreal slope, where A, B and C are complex numbers. (This version of the equation of the line was easier than the functional form this time.) And suppose the real point (c,d) and the unreal point (p+si,q+ti) are both on this line. Note that the i-arrow for this unreal point has base (p,q) and arrow extending along the vector (s,t).

Now since both points are on the line, they satisfy the equation, so

Ac + Bd = C,
A(p+si)+B(q+ti) = C.

Subtracting the first equation from the second produces

A(p-c+si) + B(q-d+ti)=0.

Multiplying this by the real number k produces

A(k(p-c)+ksi) + B(k(q-d)+kti)=0.

Adding this to the very first equation produces

A(c+k(p-c)+ksi) + B(d+k(q-d)+kti)=C.

And so the point (c + k(p-c)+ksi,d+k(q-d)+kti) is also on this line.
The i-arrow for this complex point has base (c + k(p-c),d+k(q-d)),
which is (c,d)+k[(p,q)-(c,d)]. This is a point somewhere on the line joining (c,d) and (p,q), k times as far from (c,d) as (p,q) is. The arrow itself is the vector (ks,kt) = k(s,t), which is k times the length of (s,t).

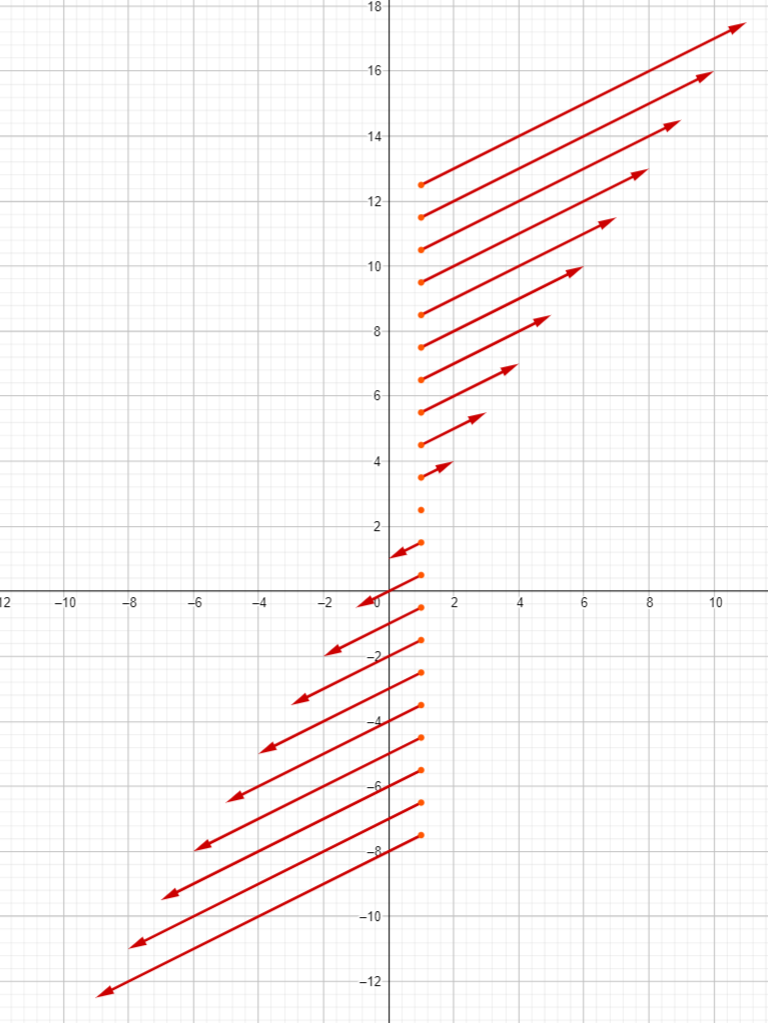
Therefore, if the base point of an i-arrow on the line is k times as far from (c,d) as (p,q), then the arrow is k times as long as (s,t).

You can see this very clearly if you freeze one of the earlier animations at the moment you can see the real point. The arrows based at points twice, three times, etc, far from the real point are twice, three times, etc as long, and pointing in opposite directions on opposite sides.

So that’s very satisfying. I’m sure more will come later.

UPDATE 2 (about 5:00am 27/7/2022)

I thought of  this one very late last night and had to wait until this morning to add it here. The previous realisation doesn’t just say that the i-arrows are longer if the base point is further from the real point on the line of unreal slope. It also says that the i-arrows with base points along a line through the real point are all parallel to each other.

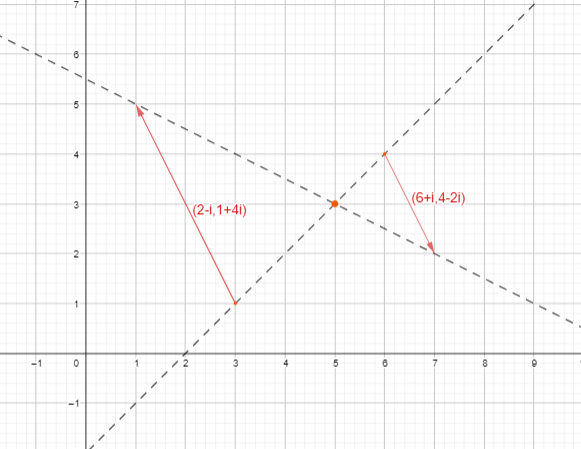
Even more so, if two i-arrows on a line of unreal slope are parallel, then the real point on that line must be on the line joining their bases, and also on the line joining their arrowheads. That’s what I realised looking at the picture above.

Here’s the calculation that proves it works.

Suppose Ax + By = C is the equation of a line of unreal slope, where A, B and C are complex numbers, and suppose (p+si,q+ti) and (a+ksi,b+kti) are both on this line, for real numbers p,q,s,t,a,b,k. Then:

A(p+si)+B(q+ti)=C,
A(a+kti)+B(b+ksi)=C.

Subtracting the first from the second:

A(a-p+(k-1)si)+B(b-q+(k-1)ti)=0.

Multiplying this by 1/(k-1)…

(Aside: I know k-1 can’t be 0, because the two i-arrows for (p+si,q+ti) and (u+si,v+ti) are the same length and direction, which means their base points and arrowhead points are on two parallel lines, and that would mean the line is actually a line of real slope.)

… gives:

A((a-p)/(k-1)+si)+B((b-q)/(k-1)+ti)=0.

Subtracting this from the very first equation gives:

A(p-(a-p)/(k-1))+B(q-(b-q)/(k-1))=C.

The point (p-(a-p)/(k-1),q-(b-q)/(k-1)) is a real point that satisfies the equation of the line! Even more, (p-(a-p)/(k-1),q-(b-q)/(k-1))=(p,q)-1/(k-1)*[(a,b)-(p,q)], so it’s a point on the line joining (p,q) and (a,b).

I didn’t actually do the calculation last night when I thought of this idea. I realised it was true, and then drew a diagram of the geometrical construction that would find the real point from two parallel i-arrows. If you join the two bases, and also join the two arrowheads, the intersection of those two lines will be the real point on the line of unreal slope! Any arrow drawn parallel to these from the line of bases to the line of arrowheads will necessarily be an i-arrow on the graph of this line. So cool!

Here are some clean accurate diagrams drawn in GeoGebra:

UPDATE 3 (about 6:00am 27/7/2022)

I really want to figure out a construction from any two i-arrows that will find the real point on the line of unreal slope that joins them. I mean, what I really want to do is figure out not just the real point, but all the other i-arrows too, but one step at a time.

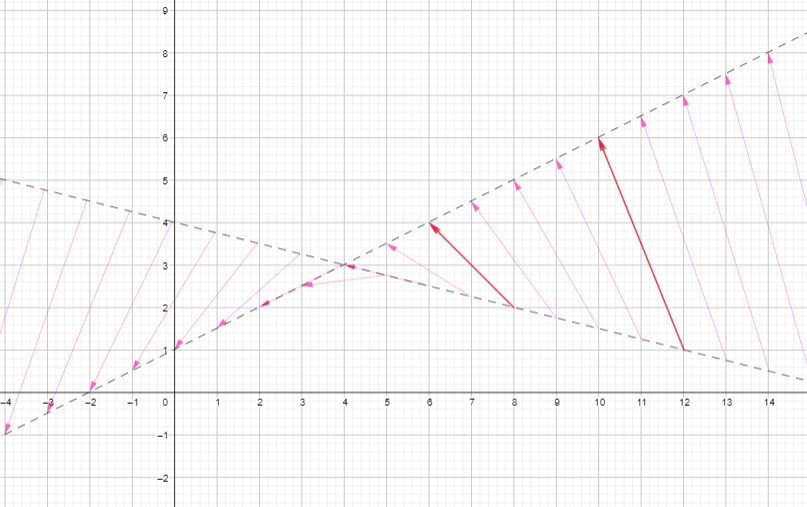
I’ve been staring at earlier diagrams of large collections of i-arrows on a line to see if I can notice anything, and I have noticed something: if you draw a line through the bases of some i-arrows, and step along this line in equal steps, then the arrowheads will step along another line in equal steps too.

This bears out with similar calculations to those above:

Suppose Ax + By = C is the equation of a line of unreal slope, where A, B and C are complex numbers, and suppose (p+si,q+ti) and (a+ui,b+vi) are both on this line, for real numbers p,q,s,t,a,b,u,v. Note the i-arrows for these points have bases (p,q) and (a,b), and arrowheads (p+s,q+t) and (a+u,b+v). Now:

A(p+si)+B(q+ti)=C,
A(a+ui)+B(b+vi)=C.

Subtracting these two gives:

A((a-p)+(u-s)i)+B((b-q)+(v-t)i)=0.

Multiplying this by any real number k and adding it to the first equation gives:

A(p+k(a-p)+[s+k(u-s)]i)+B(q+k(b-q)+[t+k(v-t)]i)=C.

Therefore the point (p+k(a-p)+[s+k(u-s)]i,q+k(b-q)+[t+k(v-t)]i) is also a point on this complex line.

The base of its i-arrow is
(p+k(a-p),q+k(b-q))
=(p,q)+k[(a,b)-(p,q)],
which is a point on the line joining (p,q) and (a,b).

The arrowhead of its i-arrow is
(p+k(a-p)+s+k(u-s),q+k(b-q)+t+k(v-t))
= (p+s+k[a+u-(p+s)], q+t+k[b+v-(q+t)])
= (p+s,q+t)+k[(a+u,b+v)-(p+s,q+t)],
which is a point on the line joining (p+s,q+t) and (a+u,b+v).

So yes it really is true that i-arrows whose bases lie on a line also have their arrowheads lying on a line too. Stepping along the line of bases a multiple k of the space between (p,q) and (a,b) will step along the line of arrowheads a multiple of k of the space between the matching arrowheads. Here is a picture illustrating how such a process produces a collection of i-arrows.

That’s what’s causing those lines of arrowheads in the animated GIFs I shared before. I’m glad I have algebra to back them up now.

UPDATE 4 (about 9:00am 27/7/2022)

I have been thinking hard about how to use two i-arrows, or a real point and one i-arrow to reconstruct all of the i-arrows on a line of unreal slope. Given the points (p+si,q+ti) and (a+ui,b+vi) on the line, you can definitely create the equation in “point-slope form”, same as you do for real lines: y=(q+ti)+(b+vi-q-ti)/(a+ui-p-si)*(x-p-si). But I want a geometrical way to do it, especially because I don’t like the look of dividing by that complex number there.

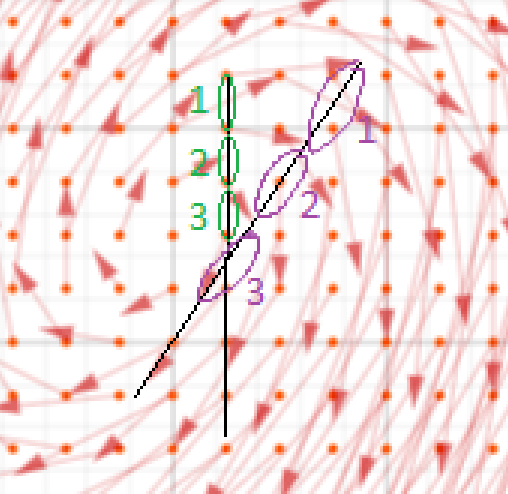
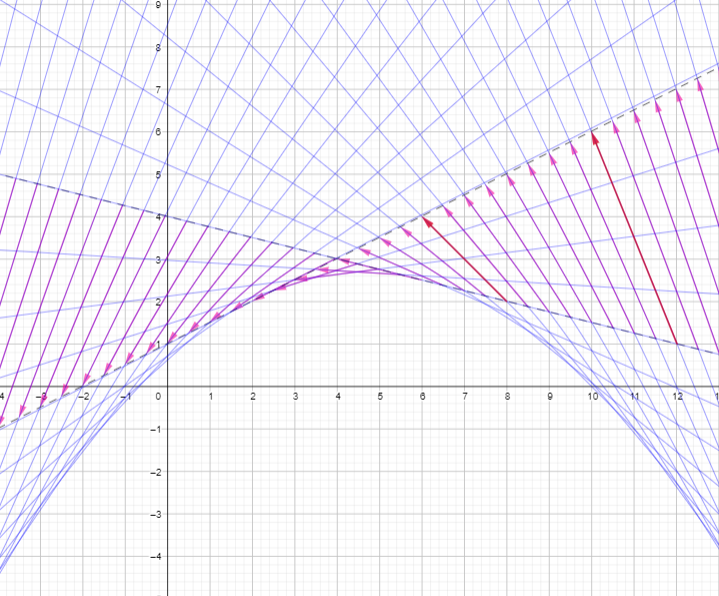
I was comparing the pictures I drew with two parallel i-arrows to the ones I was sketching with two general i-arrows. They were very similar. In both, I draw a line joining the bases and a line joining the arrowheads, and in both, there are i-arrows going from one line to the other. Surely the non-parallel ones should tell me something about where the real point on the unreal line is? At the same time I was looking at the swirl of i-arrows around the real point in those pictures of a heap of i-arrows on an unreal line, and suddenly something occurred to me: none of the drawings of the i-arrows pass through the real point! Is that actually true, or is it an artifact of my choices of which i-arrows to draw?

I started doing calculations like this: suppose (c,d) and (p+si,q+ti) both satisfy the unreal line equation Ax+By=C. Then

Ac+Bd=C,
A(p+si)+B(q+ti)=C.

Consider the line segment that is the drawing of the i-arrow for (p+si,q+ti). This contains all points of the form
(p,q)+k(s,t), for k between 0 and 1.
Can (c,d) be any of these points?

But then I realised I didn’t need to do any calculations!

For (c,d) to be on the drawing of the i-arrow, it has to at least be on the line joining (p,q) and (p+s,q+t). But I know what that line is: it’s the unique real line containing the unreal point (p+si,q+ti). And that would mean that the line joining (c,d) and (p+si,q+ti) is a real line, which I know it’s not!

So I wasn’t imagining it, the i-arrows don’t pass through the real point.

Which means when I have two non-parallel i-arrows on the same unreal line, then the space between the line joining their bases and the line joining their arrowheads can’t contain the real point on that unreal line, since that whole space is covered by i-arrows. Cool!

But I can do even more than that. The argument above actually shows the real point can’t be on any of the whole lines that are the extensions of the i-arrows. To put it more simply, none of the i-arrows point at or point directly away from the real point on the line. That’s so cool! Like, really cool!

And so even more of the plane can’t be places where the real point is. Let me see what GeoGebra has to say…

Well would you look at that. It looks like we can wipe out one whole side of a parabola. We haven’t pinned down exactly where that elusive real point is, but we’ve done a pretty fair job. I do wonder what that parabola is, but I don’t really mind too much. I’m just happy I have a bit more hope of finding that real point from a random two i-arrows.

Enough for now

Other work is pressing on me now, and I want to get down all the other stuff I had planned. So here is where I will leave it for now. I’m glad I got as far as I did. I’ve noticed some cool things, and properly confirmed them with the algebra, and made some nice constructions. Overall I think I have a much better feeling for how unreal lines work than I did before.

Further update

Later, I found how to find all the complex points on a line joining two i-arrows. You can read about it here, or follow the link below.

These are all the other posts in the series, so you can find them easily.

This entry was posted in Isn't maths cool? and tagged . Bookmark the permalink.
 

Leave a Reply