Problems with i-planes

Once upon a time in 2016, I created the idea of iplanes, which I consider to be one of my biggest maths ideas of all time. It was a way of me visualising where the complex points are on the graph of a real function while still being able to see the original graph.

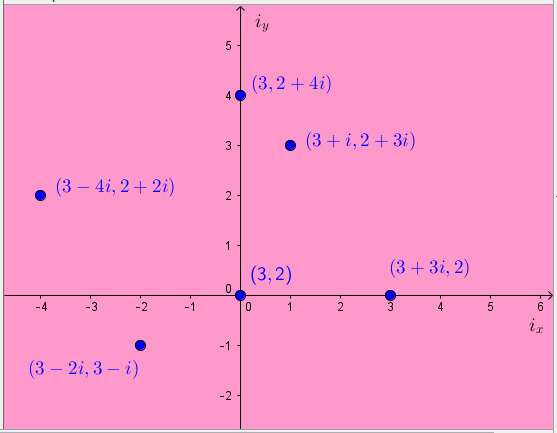
This is the idea: at every real point (p,q) of the real plane, there is a planes-worth of complex points attached, all of which have coordinates (p+si, q+ti). The collection of all the points with real part (p,q) I called the iplane at (p,q), and I imagined the iplane as a transparent sheet attached at the point (p,q) which I could flatten out to see its points when I needed to.

This was groundbreaking for me and I was so excited when it helped me find the complex points. There was a lot of cool stuff, mainly to do with taking an equation like y=x²+1, finding all the complex points in each iplane, then flattening out all the iplanes attached along a line and looking at where the points in them land. But you can already see a problem with it: the thing I want, which is to see where the complex points are (or at least look like they are) is several steps away from locating them. And when I do this process, I tend to lose the connection between the complex point and the point where its iplane is attached.

However, in my original series of blog posts, I actually already created a solution to this problem!

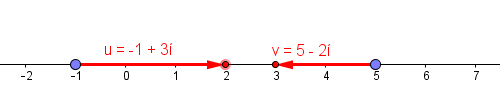
I can draw a complex number as an arrow on the real line, which starts at the real part and extends in the length and direction of the imaginary part.

This representation is not particularly useful for visualising operations on complex numbers. Addition is not too bad; multiplication is not at all obvious. What it does make obvious is conjugation. Conjugation is drawing the arrow from the same starting point in the opposite direction. This model is in fact the first time that conjugation has seemed to me like a natural thing to do.

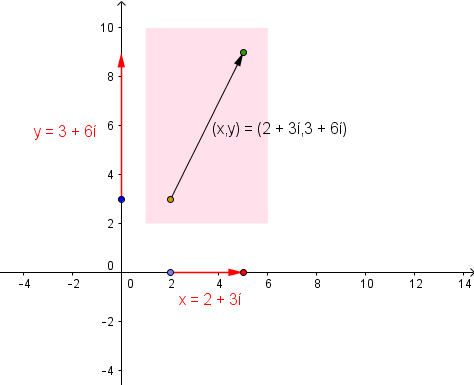
Anyway, combining this arrow model of a complex number from an x-coordinate and a y-coordinate produces an arrow in the plane. The point (p+si,q+ti) is an arrow based at the point (p,q) and extending along the journey (s,t) from there.

This is the representation I need. I have decided to call them i-arrows. I don’t want to call them i-vectors because that sounds too much like I want them to be the general powerful things vectors are. I want it to be clearly tied to the picture itself. (Plus “i-vector” is a terminology in computer science where an AI is trying to interpret spoken language, and I don’t want the wrong thing showing up when you google it.) I can show various complex points themselves more easily all on the same diagram and not lose the real point their iplane is attached to. I can still think about iplanes if I want, but I can talk about them as a collection of all possible i-arrows based at a certain point. And I can also talk about the locations of the arrowheads as opposed to the “real image of the complex point when the iplane is flattened”. I will still tend to draw the arrows in red or pink to maintain the old connection to the cellophane. I am very happy.

Introducing i-arrows

To sum up, here’s the technical details for the i-arrow representation of complex points:

• Real points are dots on the Cartesian plane, the same as they have always been.
• The complex point (p+si,q+ti) is represented as an i-arrow, which is based at the point (p,q) and extends along the vector (s,t) to have its arrowhead at the point (p+s,q+t).
• If we need it, the collection of all i-arrows based at (p,q) is the i-plane based at (p,q).

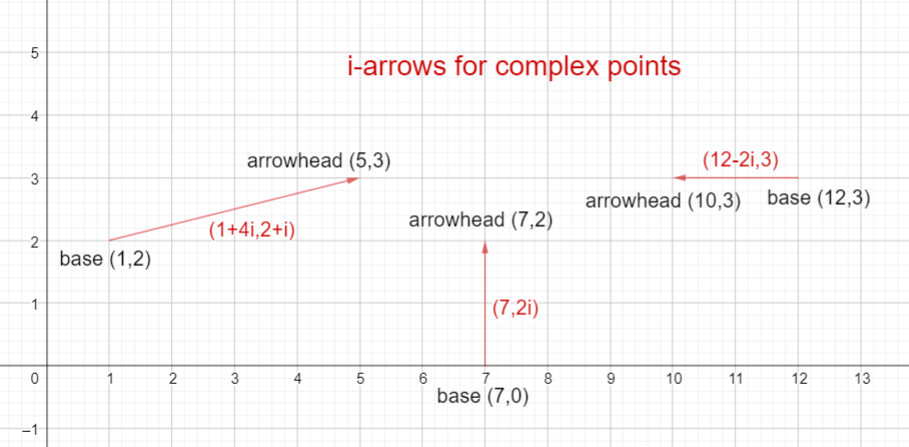
In the picture below, there are three examples of i-arrows.

• The complex point (1+4i,2+i) has been drawn as an i-arrow. Its base is at the point (1,2) and its arrowhead is at the point (1+4,2+1)=(5,2).
• The complex point (7,2i) has been drawn as an i-arrow. Its base is at the point (7,0) and its arrowhead is at the point (7,0+2)=(7,2).
• The complex point (12-2i,3) has been drawn as an i-arrow. Its base is at the point (12,3) and its arrowhead is at the point (12-2,3)=(10,3).

Working and playing with i-arrows

When I started this blog post, I was going to show you everything I’ve been working on and playing with using i-arrows, but when I came to organise it, I thought more about it and made more stuff, and it got bigger and bigger. So I am putting all that other stuff into later blog posts. The current plan is the following:

• Where the complex points are: i-arrows (YOU ARE HERE)
• The complex points on a line using i-arrows
• Further updates on the complex points on an unreal line using i-arrows
• The complex points on a line in finite geometry using i-arrows
• The complex points on a parabola using i-arrows
• The complex points on real circles using i-arrows
• The complex points on unreal circles using i-arrows
• The line joining two complex points using i-arrows

I have to admit to a little sadness at my original idea of iplanes fading into the background as this new idea asserts its usefulness. But it may become useful again one day and it will still hold a special place in my heart. And really, looking at what the i-arrows can do, I am feeling very happy too.

Acknowledgement

Thanks to Dr David Roberts for listening to me talk about all of this, and suggesting the terminology “base”.