I was going to have a punchy title for this post, with a big moral to apply to the future, but I’ve decided I’m just going to describe to you what happened yesterday as I tried to learn some Genetics. You see what you can learn from my experience.
Yesterday I was helping out at the workshops for the Veterinary/Animal/Plant Science course “Genes and Inheritance”. During this workshop, one of the things they were doing was using the following formula:
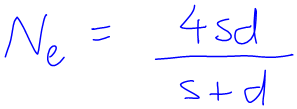
The formula was written nice and big on the whiteboard and was more-or-less meaningless to me. I remember seeing it when I prepared for the workshop about a month ago and telling myself I should look it up in the lecture notes, but I confess I never did so.
I went up to one of the workshop leaders and asked her if she could tell me what each bit of the formula meant. I pointed to each symbol and asked what it was.
The Ne stood for “effective population size”. Ok. This must be a way to convert the actual population size to some other size in order to compare them in some way. I decided I’d wait until I found out more about the rest of the formula before I sort out why we’re doing that.
The s stood for… well I thought she said size, and so I asked “the size of what?”. After a quizzical look from her, and a couple of exchanges back and forth, I realised that the word was in fact “sires”, as in the number of breeding males. I suppose I should have expected something like that. The d stood for “dams”, which is apparently the corresponding word for breeding females.
Ok. So the calculation uses the number of males and females in a population to calculate a new “effective population size”. I asked what this effective population size told us about the genetics, and was informed that small effective populations are indications of a high amount of inbreeding. Yes, I suppose that makes sense — a small population would have to have lots of inbreeding.
So I understood what the formula was about.
Only the more I looked at it, the less I understood. Why is there multiplication on the top and addition on the bottom? Why is there a 4 there? Why does this produce the effective population size? What does “effective population size” really mean?
This continued to puzzle me on-and-off during the first workshop, but mostly off, because I was helping students with the rest of the questions, and it was driven out of my mind by something else I noticed: the worrying tendency of students to use a formula, when you could solve the problem by drawing a quick picture/table and using a bit of reasoning. They’d ask me, “which of these is p and which is q?”, and I’d respond that I didn’t actually know, I was just doing my calculations based on where the numbers were in my drawing, not based on a formula with specific letters. When I sat down to figure out which thing corresponded to which part of their formula, most of them were happily amazed that the formulas that had been previously given them no information, suddenly told them a story about the strucure of genetics.
After this happened for the fifth time, I realised that this was precisely my problem with the effective population size formula: it was meaningless. It told me no stories about genetics, but simply told me how to calculate something.
By this time I had seen students using the formula and telling me useful things they knew about it. For example, they told me that if there were the same number of sires and dams, then the effective population size would come out to the same as the real population size. And they also told me that an unequal distribution of males and females would result in a lower effective population size.
I could see the thing about the equal sizes with a quick bit of algebra:
![If s=d, then N_e = (4s^2)/(2s) = 2s = s+d = actual population size]](https://blogs.adelaide.edu.au/maths-learning/files/2015/10/Ne-4.png)
But again it was hardly telling me why the formula was there in the first place. There are any number of formulas that could do that trick!
The actual question they had to work on involved them finding out how many sires there would have to be in order to get Ne = 50, if you knew there were 10 times as many dams as sires. This got me thinking that perhaps you could rearrange the formula to be about the proportion of males and females rather than the raw number. Some fiddling around got me this:
So you could rewrite the formula in terms of the proportion of males and females, and the new formula had a kind of pleasant simplicity about it. It even said that Ne was a multiple of N, which matched what I was told about it being smaller than N.
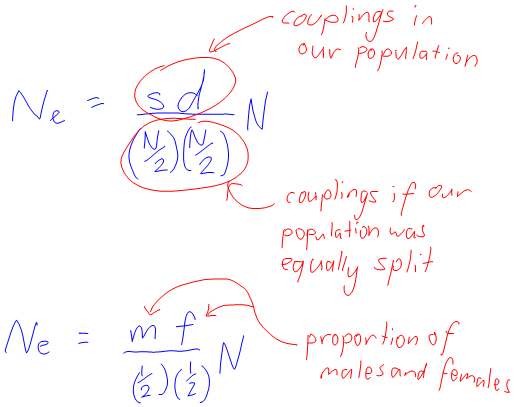
I asked the workshop leaders about this, and they had never seen anything like it. One of them, though, said they could explain why the sd was in the original formula: it was about the number of male-female couplings in the population. If there are s males and d females, and any male can go with any female, then there are sd possible couplings. She also pointed out that it had something to do with the fact that the effective population size is the real population size when there’s the same number of sires as dams. So maybe we should be comparing to the same size population, but with equal proportions!
Thinking about my own formula, if s and d were equal, then the proportions would be 1/2 and 1/2, so if you multiply them you’d get a 1/4, which would neatly cancel out the 4. This calculation followed:
That made a lot of sense. But the couplings were bothering me, so I did this too:
![(sd)/[((s+d)/2)((s+d)/2))] = (4sd)/(s+d)^2; N_e = (4sd)/(s+d) = [(4sd)/(s+d)^2](s+d)](https://blogs.adelaide.edu.au/maths-learning/files/2015/10/Ne-7.png)
So that worked too! Basically, I was comparing the number of couplings in the population to the number of couplings in the same population but equally distributed, and the fraction produced is how I adjust my population size to get the effective population size.
I checked it with a numerical example: try s=10, d=20, then if it was equally split they’d both be 15. So…
That’s pretty cool, actually. And not just that, it’s something that I can remember because it makes sense to me.
I still wanted to make sense of the proportions version, though, plus I was interested if anyone commonly explained it in terms of pairings. So I went looking online when I got home. I tried many search phrases and found no places where the derivation of the usual formula was given. I learned along the way that “sex ratio” was the most common terminology for this concept of the number of males and females affecting the effective population size. Plus, most of them refer to Nm and Nf rather than s and d.
After more digging and scanning actual research papers that used effective population size in practice, I found some referring to Ne/N. This seemed promising, since my version of the formula could be arranged that way. Interestingly, despite people wanting to calculate Ne/N, no-one actually gave a formula for it directly, which I found most unusual.
Finally, I found a book with an explanation, though wildly different to the one I was looking for! This one was all about the probability two of your four grandparents actually being the same person, and of your half-brother-and-sister parents passing on repeated genetic information to you. The 1/4 comes about because of the 1 in 2 chance of getting your common-grandparent genes from each parent. And the formula is actually a rearrangement of 1/Ne = 1/4(1/s+1/d), and I still can’t find any explanations using couplings.
At the moment, the best I have is that the proportions version is just a relocation of the N’s in the raw-numbers version.
Standardising to proportions is not such a bad explanation, though it would be super awesome if there was a better explanation.
I’ll take the ones I have though:
(PS: If anyone can think of a useful moral for this tale, please do let me know!)

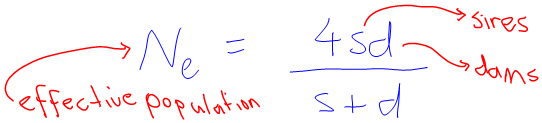
![N_e = (4sd)/(s+d) = (4sd)/N where N is total pop = 4(s/N)d = 4(s/N)(d/N)N = [4(s/N)(d/N)]N = 4mfN, where m is prop of males and f is prop of females](https://blogs.adelaide.edu.au/maths-learning/files/2015/10/Ne-5.png)
![N_e = 4(s/N)(d/N)N = [[(s/N)(d/N)]/(1/4)]N = [(s/N)(d/N)]/[(1/2)(1/2)]N](https://blogs.adelaide.edu.au/maths-learning/files/2015/10/Ne-6.png)
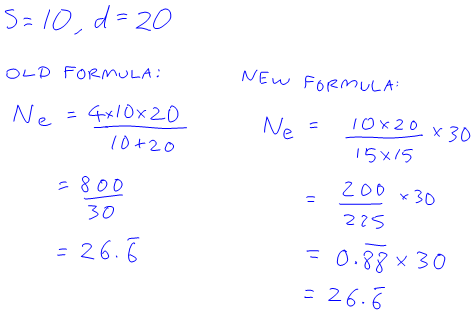
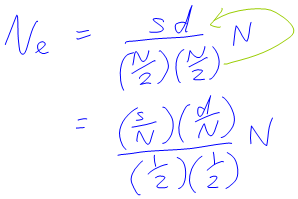
I think that this story is a great application of Galileo’s remark about “maths being the language in which the universe is written”.
In addition to the probabilistic interpretation, your product of proportions, m*f, for large and well-mixed populations, also relates to the “Law” of Mass Action. So such terms can appear in differential equation models involving interactions between 2 different “species”.
In conclusion, I think this is a really cool story about describing real processes using maths.