This is the second in what has turned out to be a series on Where the Complex Points Are.
- Where the complex points are: introduction to the iplane concept
- Where the complex points are: on a line (YOU ARE HERE)
- Where the complex points are: on a parabola
- Where the complex points are: the graph of a function
- Where the complex points are: where the idea came from
In the introduction, I described the place where the complex points are: at each point (a,b) in the real plane, there is an iplane attached, which contains all the points (a+ci,b+di). These points are arranged with the x-axis showing the imaginary part added to the x-coordinate and the y-axis showing the imaginary part added to the y-coordinate. I imagine them as being a transparent sheet attached to the point itself and being able to be flattened out to sit on top of the real plane.
In this post, I want to talk about where the complex points are on a line. This is the first reason why this representation of complex points is so very cool.
A real line
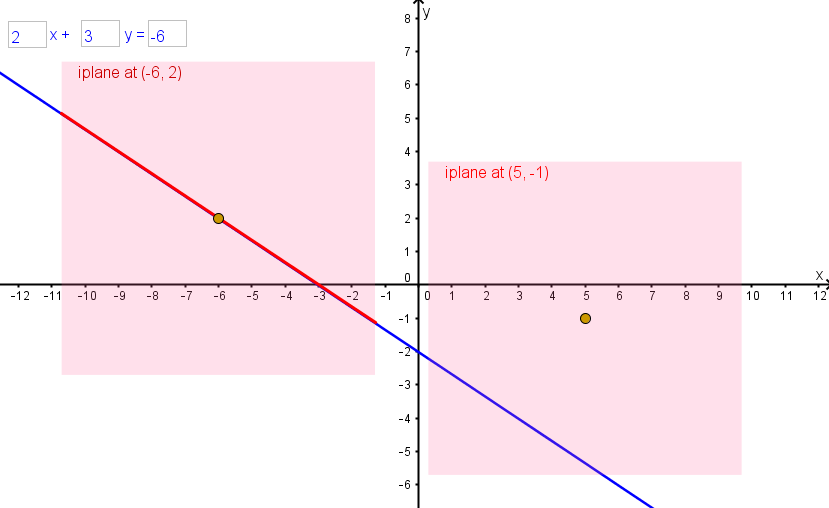
Every real line has an equation like ax + by = c for some real a, b, and c. For example, 2x + 9y = 7, -3x + 5y=8, x – 2y = 3, x=4 and y=5. (I’ve used whole numbers here but there’s nothing stopping us using fractions or square roots or transcendental numbers like e.)
But we know that at every point there is an iplane attached which holds all the complex points. Which of these complex points are part of the line? First we need to remind ourselves that a point is on a line when it satisfies the equation of the line. That’s fundamentally what an equation is for: deciding if a point is part of a set or not.
Let’s consider the line x – 2y = 3…
- The point (3,0) is on this line because 3 – 2*0 = 3.
- The point (1,-1) is on this line because 1 – 2*(-1) = 1+2 = 3.
- The point (9,3) is on this line because 9 – 2*3 = 9-6 = 3.
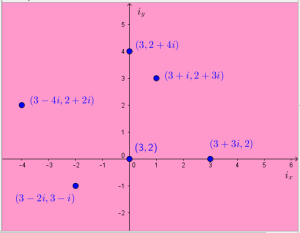
- The point (3+2i,i) is on this line because 3+2i – 2*i = 3+2i-2i = 3.
- The point (1+4i,-1+2i) is on this line because 1+4i – 2*(-1+2i) = 1 + 4i +2 – 4i = 3.
- The point (9-10i,3-5i) is on this line because 9 -10i -2*(3-5i) = 9 – 10i – 6 + 10i = 3.
There is a pattern forming here: in order to get my complex point to be on the line, I need to make sure the imaginary parts are the right sizes so that they subtract away when I put them in the formula. The real parts have to create the number 3 I need as well, which means the real parts have to satisfy the original equation.
Let’s do this with algebra:
What does this mean? If the point (p+ri,q+si) is on the line with equation ax + by = c, then the point (p,q) has to be on the line. This means that all the complex points on the real line are in the iplanes at the points on the real line. That’s very pleasant — the complex points on this line are in some way attached to the line itself, because they’re in the iplanes attached to this line.
But it gets better! The complex point (p+ri,q+si) is the point with coordinates (r,s) in the iplane at (p,q). And the point (r,s) has to satisfy the equation ax + by = 0. That means the point (r,s) lies on a line parallel to our original line passing through the centre of the iplane. When you take the iplane at the point (p,q) and lay it flat on the real plane, the complex points in that iplane that are part of the line will lie on top of the existing real line! This is because they are on a line parallel to this line passing through a point on this line.
So in our representation, the complex points on a real line aren’t just in the iplanes attached to the real line, they look like they are actually on the line! Isn’t that cool?!!
You can play around with the iplanes attached to real lines in the following GeoGebra applet.
A line with real slope
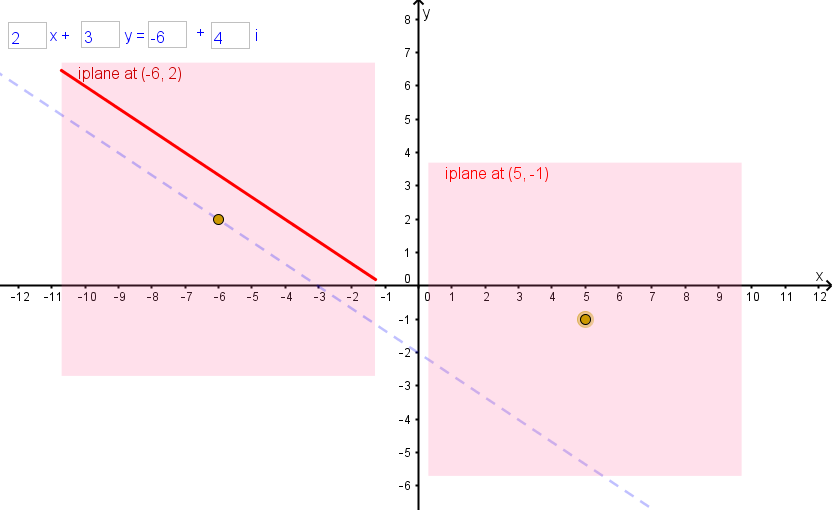
There are a whole lot of lines in the complex plane that aren’t real lines. The first kind I want to deal with is those with real slope. That is, their equations are of the form ax + by = c + fi for some non-real number c+fi and real numbers a and b. This kind of line has no real points at all – it’s not possible to put real numbers into ax + by and get a non-real result. But where actually are all the non-real points on this line?
So, the points on the line with equation ax + by = c + fi are in the iplanes attached to the real line with equation ax + by = c, and in each iplane they form a line parallel to this real line. In fact, if you look at where they are across all the iplanes, they all form the same line parallel to the real line.
You can investigate these kinds of lines using this GeoGebra applet.
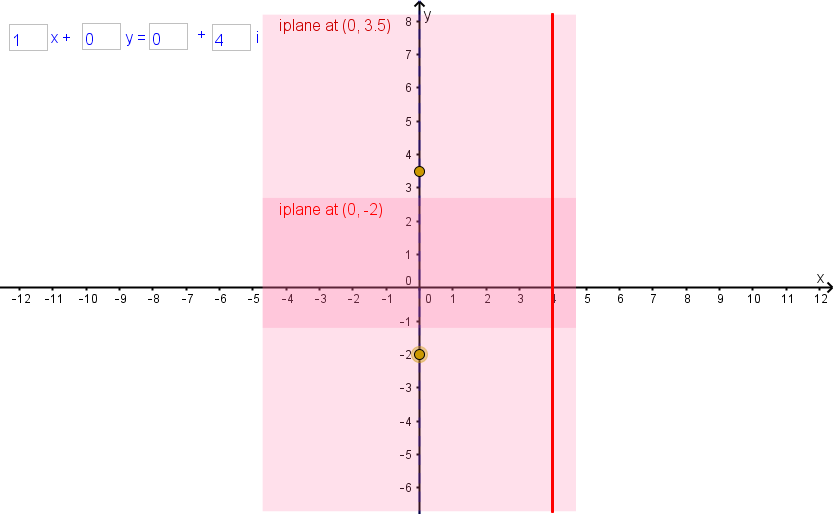
Of particular interest for our purposes later on are the “vertical” complex lines with equations of the form x=fi. The points on this line are in the iplanes attached to the real line x=0 — that is, they’re in the iplanes attached to the y-axis. Inside each iplane they form a vertical line, which looks like it’s part of the real line x=f.
A line with unreal slope
The last kind of line is a line with unreal slope. It would have an equation like (a+di)x + (b+ei)y = c+fi. You’d need to make sure that a+di and b+ei weren’t related by a real multiple or you could divide by some complex number to produce real coefficients for the x and y — we’ve already covered lines like that. In fact, it must therefore be possible to arrange it so that the y-coefficient is 1. In that case, we might as well write it in “slope-intercept” form, which might be a bit easier to process. So let’s take a look at the line with equation y = (a+di)x + (c+fi).
Hmm. That’s not particularly edifying. What does that mean? Why don’t we pick an iplane and see what the points on our line look like in this iplane:
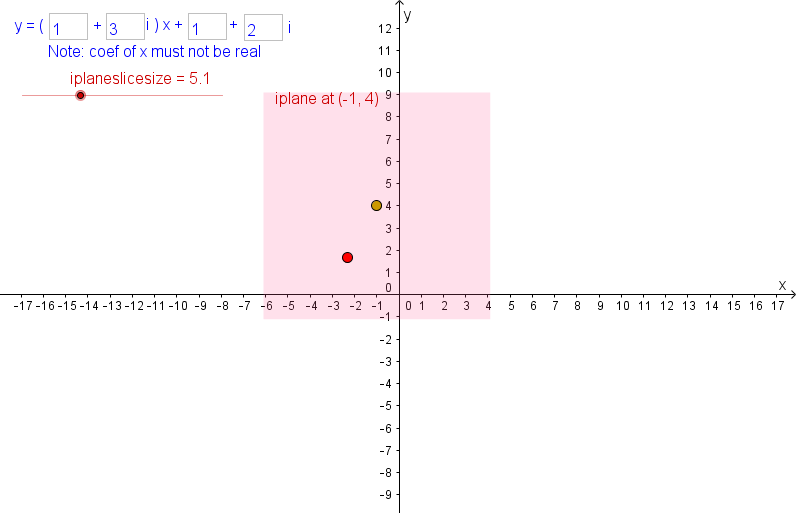
This means that given (p,q), we can find a unique value of r. Substituting this into the other equation gives us a unique value of s. That is, every iplane has exactly one point of this complex line! You can investigate what these points look like with this GeoGebra applet.
Note that there is in fact exactly one real point every line with complex slope. Using the notation above, it’s the point (-f/d, -af/d+c). It’s quite hard to find the point by trial and error in the GeoGebra applet!
Conclusion
So there you have it. Using iplanes, the lines with real slope actually look like lines, and the lines with unreal slope are a cloud of points with one in each iplane. In the next post, I’ll talk about parabolas…




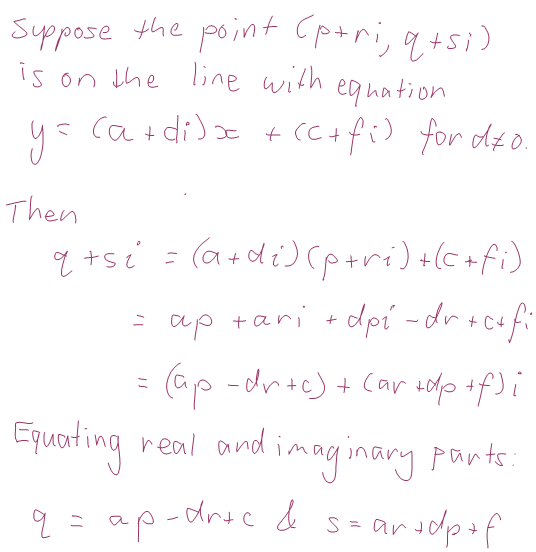
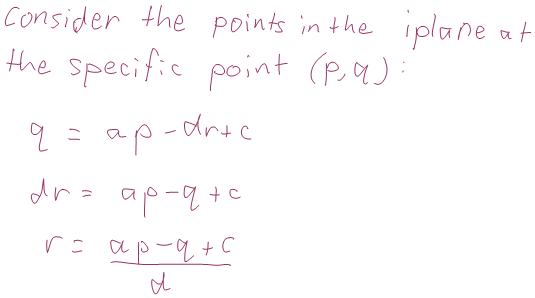
[…] Where the complex points are: on a line […]
[…] Where the complex points are: on a line […]
[…] Where the complex points are: on a line […]