What trig subsitution is
Trig substitution is a fancy kind of substitution used to help find the integral of a particular family of fancy functions. These fancy functions involve things like a2 + x2 or a2 – x2 or x2 – a2 , usually under root signs or inside half-powers, and the purpose of trig substitution is to use the magic of trig identities to make the roots and half-powers go away, thus making the integral easier. (I say “easier” by which I mean “not impossible” as opposed to “simple to do”. The resulting integral is usually not simple and usually involves attacking an integral that now has a whole lot of trig functions in it. Moreover, the stage where you put your original variables back in is often a lot fancier than in other substitutions and involves trig identities yet again.) The Mathematics 1A students at my university learned it in recent weeks and are struggling with it in various ways, not least of which is the sheer amount of paper it takes to write it up properly!
Remembering which trig substitution to do
One particular thing the students struggle with is choosing which trig substitution to do. Actually, they tell me they have trouble remembering which trig substitution to do, which I think says a lot about how this topic is presented in most resources.
When I google “trig substitution”, every page that comes up presents me with a table very much like these:
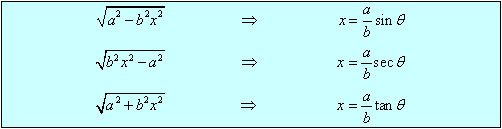
From Paul’s Online Calculus Notes http://tutorial.math.lamar.edu/Classes/CalcII/TrigSubstitutions.aspx

From S.O.S Math http://www.sosmath.com/calculus/integration/trigsub/trigsub.html

From Wikipedia https://en.wikipedia.org/wiki/Trigonometric_substitution
The examples that follow these tables usually give no reason at all why the particular substitution was chosen, or just say it’s “easy to see”. This implies that in order to choose which one to do, you look it up in the table and then do the one you find.
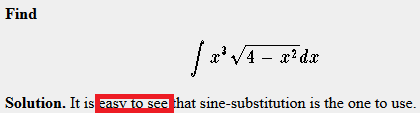
From S.O.S Math (emphasis mine) http://www.sosmath.com/calculus/integration/trigsub/Example1/Example1.html
And if there is no table to look up (such as during the maths exam) then of course you would just have to remember.
Choosing which trig substitution to do
When I first learned trig substitution, I also struggled to remember which one to do in a given situation. Even now I can’t remember — I simply don’t do them often enough to be fluent in just knowing the right one off the top of my head, and the stimulus-response nature of looking it up in the table just seems hollow to me. As a student I never really knew why each format implied that a particular trig substitution had to be done. I could understand each step in the working for any example, but I still couldn’t see how the decision had been made. A student in the MLC last week expressed this exact frustration last week — he could see that the forms matched the forms in the table, but he wanted a reason why.
Much much later I realised that the fact the working worked at all was the actual reason why the particular substitution had been chosen! This was what eventually freed me from having to remember. Since the working working was what made the decision, and since I had to do that working in order to finish the problem anyway, I could just get going and make the decision of which one to do along the way. Note that one reason I have trouble remembering them is that I also don’t remember all the versions of the squared trig identities off by heart, I just create them starting from (cos x)2 + (sin x)2 = 1. This new method allowed me to just continue doing that and it actually supported my success.
Here are a couple of examples of me deciding which trig identity to do along the way that I did in revision seminars this semester.
So that’s how I choose which trig substitution to do. I try to construct a trig identity that matches what’s in my square root as closely as possible, and then by the time I’ve done this, the substitution is chosen for me and part of the work is already done.
It works for me, anyway.

I use word association to remember which trig sub to use.
When I see a + sign, that looks like the letter ‘t’ so I know to use tan sub.
When I see a^2 – x^2, that is Subtraction that starts with an ‘s’ and so does sine function. “A ‘s’ is my sign to use sine.”
When I see x^2 – a^2, that also is Subtraction, so it will be either Sec or Sin function. I remember tmto use Sec here because the equation starts with an ‘x’ that sounds like sex and I always think of sex when I see secant abbreviated as secx.
I know, it sounds ridiculous and weird, but that is how I remember which one to use.
Watch “Integration: Trigonometry Substitution / By M J Iqbal” on YouTube
https://youtu.be/XmSCnRogOUY