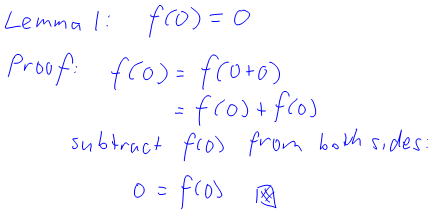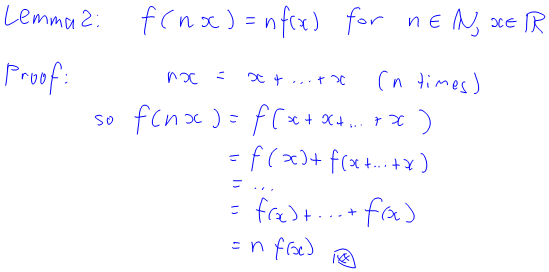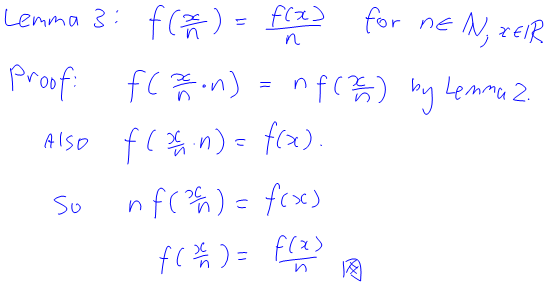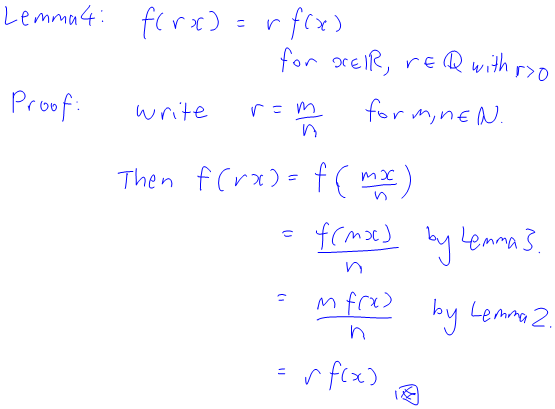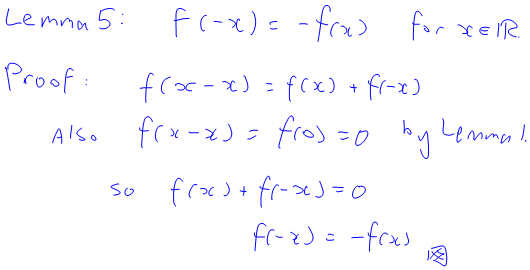There is a very common thing that students do that causes pain, distress, confusion and depression in any maths educator who witnesses it. Both the error itself and the educator’s response to it are very clearly described by this excellent picture from the blog “Math with Bad Drawings”:

Distributing wrongly over plus, from Maths with Bad Drawings
Every single one of the statements in that picture is horrifyingly wrong, but students do them all the time. At least one of the regulars in the MLC took a good three years to learn not to do this with square roots, despite being very clever with all sorts of high level maths.
It is, of course, not the students’ fault. The fact that it happens so often must mean that it is a natural response to learning the symbolism of maths. In the blog post, the author surmises that one reason students do this is that they think that distributivity is a property of brackets rather than a property of multiplication. Students have actually told me explicitly that the reason they did these was because of the brackets being there. Another reason is that students don’t know what function notation is, and actually think that it is multiplication. I have lost count of the number of students who say “sin times x” and “ln times x”, and who talk about “dividing by ln” when they solve an equation like “ln(x) = ln(2)”.
It seems one thing we need to do is be careful about the way we speak so that students don’t get the wrong impression. For example, perhaps instead of saying “expand the brackets” we should say “expand the multiplication”. Also, we need to be very very explicit on a continual basis about when brackets are being used for function inputs and when they are being used for multiplication. The notation itself is ambiguous and we need to explicitly point out the ambiguity.
But there is one final problem. There are plenty of students who know that distributivity is a property of multiplication, and who know the difference between function notation and just brackets, but still attempt to distribute all sorts of things over addition. The student I mentioned above is one of them. Somehow, the pull to distribution is very strong even if you know the difference between brackets and function notation. How do we help these students?
Certainly every time we give them a new function we can tell them what it does and does not distribute over, and so create a list of things which don’t distribute. This list is very long, so it would be so much more productive if they had a list of functions that do distribute. Well it turns out there is only one thing on the list! The ONLY reasonable function of real numbers that distributes over plus is multiplication by a constant! I have had a lot of success helping students not to distribute wrongly by telling them that there is precisely one situation when they can distribute correctly. It clears away all the long list of “don’t”s and replaces it with one single “do”.
For those of you who are interested, here’s a proof (a PDF version can be found here):
(Note for seasoned functional analysts: I have used the fact that the function is continuous to make the final jump from the rationals to the reals. You don’t actually need the strength of continuity to do this jump: you can use different arguments to do this jump under different, weaker assumptions on the function. It could be increasing, or decreasing, or integrable or measurable and you can make it work.)