The community of maths users the world over agrees that when evaluating an expression or calculation, some operations should be done before others. Mostly it’s to prevent us having to be needlessly specific about what order to do calculations in, mathematicians being very concerned with efficient communication.
When you learn it at school, it usually goes something like this:
- Brackets (and other grouping symbols), from innermost out.
- Exponents (also known as powers).
- Multiplication and Division, working left-to-right.
- Addition and Subtraction, working left-to-right.
The name I learned for this order of operations was… the Order of Operations. Many other people call it BODMAS, BIDMAS, BEDMAS, PEDMAS, PEMDAS, and other similar combinations. I remember coming to university in Adelaide and my new South Australian friends kept saying “BODMAS” and I had not the slightest clue what they meant. Even now I don’t like using the acronym as the name for the concept itself.
My problem with the order of operations as stated above is this: it’s wrong! It’s wrong because you almost always don’t do the operations in the order described. You don’t do all the multiplications before all the additions, and instead will often quite a few of the additions first because they are easier. And you don’t do the multiplications in the order they come, but rearrange them into some other easier order. And you often don’t do the brackets first, but instead choose expand them out in order to make the calculation easier.
If you followed the order of operations to the letter as it is usually described, you will have a very inflexible way of approaching calculations, which will enforce quite a bit of unnecessary and difficult work. Take the simple calculation 3 ÷ 2 × 4. I know that I can multiply the 3 and the 4 before doing the dividing by 2, which greatly simplifies my working compared to having to divide the 3 by the 2 and then multiply by 4. A large number of students who know BODMAS don’t realise they are allowed to do this sort of thing.
What we experienced users of maths use is not a rigid set of rules for the order to calculate in, but a set of rules that tells us when we can be flexible and still produce the same result. Things like “if it’s all + then do it in any order” or “if it’s all × and ÷ then you can do all the things after × signs in any order”. I like to think of the operations as a sort of glue, and some operations have a stronger glue than others. Addition is the weakest glue, with subtraction only marginally behind because it sticks to the things to its right. Powers have the strongest glue, after brackets, which are really more like sticky-tape.
In my head, the order of operations isn’t even in words at all. It’s much more like this picture:
or this simplified version:
Whenever I teach students one-on-one about doing calculations, we talk about what ways there are to be flexible so that they can choose more efficient methods, and I draw these pictures. It seems to help them be more flexible rather than blindly follow an order that restricts them.

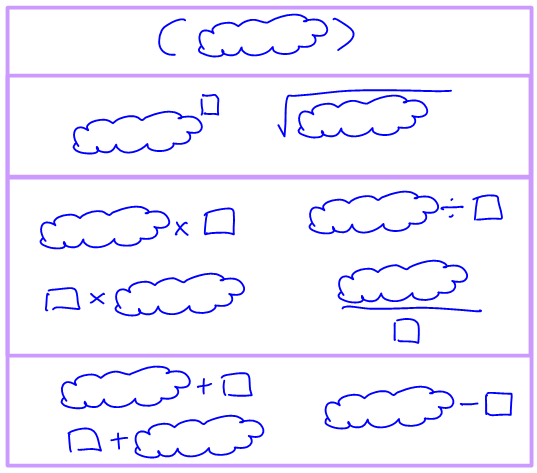
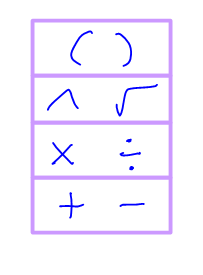
Effective and easily accessible discussion about Order of Operations. Thank you David…this is a useful resource to support Maths teachers.
In working with students, I use ‘doing’ and ‘undoing’ (borrowed from John Mason) as a metaphor to tune them into using inverse operations.
[…] I were to actually do this calculation. This is the “order of operations”. I’ve written about it before, but I’ve moved on in my thinking quite a bit since […]
Brackets Of Division Multiplication Addition Subtraction
This is what was taught in Adelaide schools during the 1970’s.
When dividing, it was implicit that everything to the right of, or below the divide sign, was considered in brackets to be evaluated first. This becomes the DIVISOR.
For example:
6 ÷ 2(2+1) = 1
=> 6 ÷ (2(2+1)) = 1
There is no alternative answer.
Mate, not everyone uses the same rules for this, you know! And this is not at all what my blog post was even about. It was about being more flexible, not being more rigid.
2+3×4=14 this is correct
Your way??
2+3=5, 5×4=20 ?? This is incorrect
Don’t teach my kids 😂😂😂😂😂
No, my way also produces 14 for 2+3*4. The bottom of the tower is the bit you do last, so the addition is done last, just like you did.