Once upon a time, I did a PhD in projective geometry. It was all about objects called quadrals (a word I made up) – ovals, ovoids, conics, quadrics and their cones – and the lines associated with them – tangents, secants, external lines, generator lines. During the first two years, I did talks about my PhD research, which I could not resist calling “David Butler and the Philosopher’s Cone” and “David Butler and the Chamber of Secants”.
At that time, my use of JK Rowling’s titles had to stop because there was no suitable mathematical thing to insert into the third title. It’s been ten long years since “David Butler and the Chamber of Secants”, and finally I have found something to use. Hence, welcome to…
David Butler and the Prisoner of Alhazen
Chapter 1: In which David finds out about lunes for the first time
As you may have noticed, I have quite a love affair with the Quarter the Cross problem, having blogged about it here and here. This blog post is not about Quarter the Cross, but the story did start there.
At the December holiday One Hundred Factorial session, we did Quarter the Cross together, and these were some of the solutions we came up with:
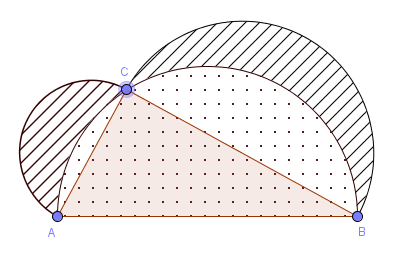
You may notice some rather interesting solutions involving curved shapes. Well, one of the students (Adam) created the first of these, and of course we all asked him how he was doing it. He told us the shapes were called “lunes” and showed us how to draw them: you draw semicircles outside the short sides of the triangle, and then one big semicircle inside the longest side, which has to go through the point because semicircles on hypotenuses always pass through right angles. Then he declared that the area of the two lunes was the same as the area of the triangle. (That is, in the following triangle, the striped area is the same as the pink area.)
Of course we needed a proof of this, and we duly worked together to construct one. Here’s a pretty version of the proof we came up with:
Later that day, I tweeted about this, and someone asked what this theorem was called. I didn’t know, so I went looking online for more about these things. My first problem was that I was searching for “loons” instead of “lunes”. Afterwards, it made perfect sense that they were called “lunes”, since “lune” is the French word for “moon”. But when I was searching, I had only heard the word spoken aloud and not seen it written down, so I couldn’t know that it was actually a French word could I? After what seemed like hours, I finally did find it. I was not disappointed.
These things have the coolest name of any maths object I know, worthy of any Harry Potter title: the Lunes of Alhazen! They are named after an Arab mathematician/scientist/philosopher who lived about a thousand years ago, and was once so famous that if you simply said “The Physicist” then people knew you were talking about Alhazen. (Funny how most of us educated in Western countries have never heard of him.)
Chapter 2: In which David is imprisoned by Alhazen’s lunes in two different ways
But the story didn’t stop there. As with most very cool maths things, it sort of takes over a corner of your mind, holding you prisoner, as it were. This Alhazen and his lunes held me and others prisoner in various different ways.
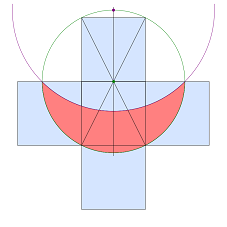
One way I was held prisoner was that I found myself trying to see lunes everywhere. Every time I saw a right-angled triangle in a design, I’d wonder about the two lunes you could make from it. MLC staffer Damien confessed this same obsession to me not long after the One Hundred Factorial session, except that he was actually carrying a pair of compasses around to do the actual construction. In Quarter the Cross itself, I had quite an ambition to find a single lune that had an area of a quarter of the cross. I did find it, and here it is:
(Technically, this lune is the Lune of Hippocrates. You can make two of them as lunes of Alhazen on the short sides of an isosceles right-angled triangle, but one big one can be drawn on the hypotenuse too, to give the same area.)
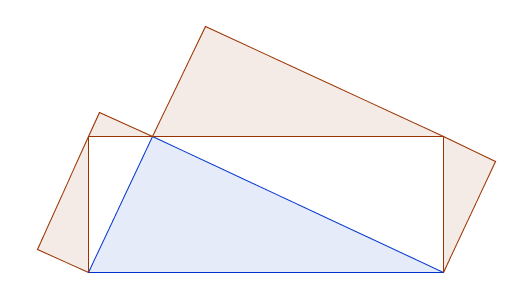
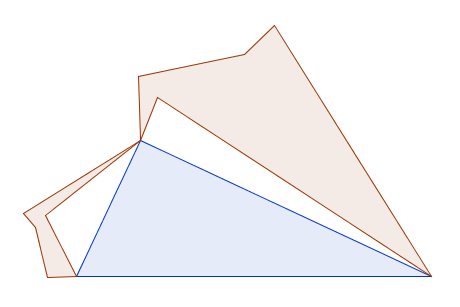
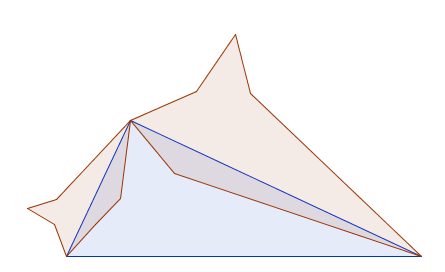
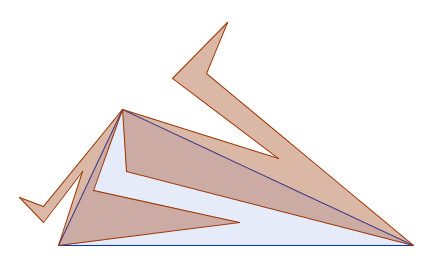
The other way the Lunes of Alhazen held me prisoner began when I realised that our earlier proof didn’t rely on the fact that the shapes I had drawn were semicircles. I could use any shape as long as they were all similar to each other, because the areas of similar shapes are always proportional to the squares of matching lengths. So I started thinking about the concept of the “Things of Alhazen” – objects constructed in this way from a right-angled triangle. Here are a few:
And a few more, after I realised they could go inside the triangle too.
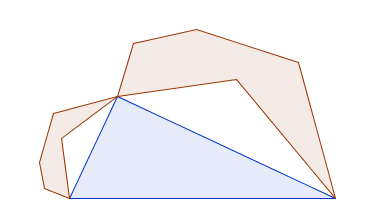
And a few more, after I realised the big shape didn’t technically have to go through the right-angle.
(Note they’re all polygons because I was doing them in Geogebra and it was the easiest way to colour things in the way I wanted. I suppose I could have done it in Geogebra and copied the picture and bucket-filled, or drawn them in some other program. But this is what I did.)
Chapter 3: In which Tracy is also a prisoner of Alhazen
But I wasn’t the only one who was imprisoned by these lunes of Alhazen. This week it was “Twitter Math Camp”: a conference where those in the MTBoS come together to share their reflections and learning, organised by teachers for teachers. At TMC, Tracy Zager did a keynote talk where she talked about the benefits that happen when people at all different levels of education come together to learn about teaching maths from each other. (You can see the part of the video directly related to this story here, and see the slides or give comments to Tracy at her blog here.)
Tracy told the story of Quarter the Cross, and how it leaped up and down the levels of education and back and forth around the world. When she originally saw the work me and my students did, she was instantly caught by the curved shapes, and wanted to know more. Upon hearing the name of them, this was her response:
The "Lunes of Alhazen?" Are you kidding me with this? Beautiful math and a rad sci-fi sounding name? Day made! https://t.co/m4zBbXtZT7
— Tracy Johnston Zager (@TracyZager) December 16, 2015
She was instantly captured by the wonder and the history and the awe, just as I was. But the imprisonment is deeper than this.
That tweet was seven months ago, and yet here is Tracy in a keynote talk at a conference, remembering this as a key moment in her journey as a maths educator. In a way, Alhazen has captured a part of her memory. She will forever think back to this time and have it all wrapped up in these lunes. And so will I.
We are prisoners of Alhazen in the best possible sense.


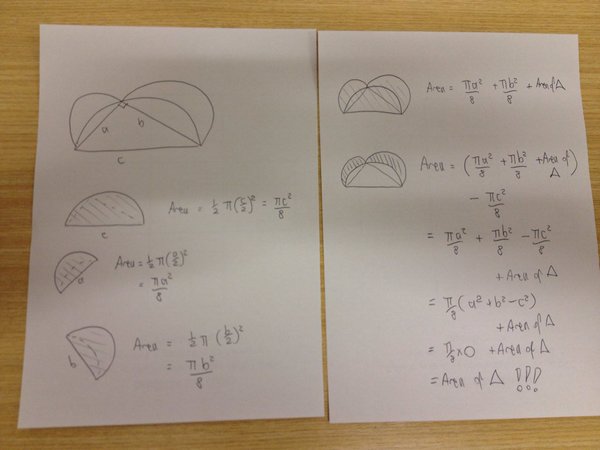
Thanks for this. These are so cool they are almost magical.
Earlier today I was catching up with the #TMC16 and viewed Tracy Zager’s Keynote Video. The Lunes of Alhazen really jumped out at me. I am excited to bring this to my students this year, along with the Quarter Cross. I believe that after this past summer’s negative incidents, and our coming together in Rio this August, I feel as an educator to stretch and find connections btwn mathematics derived within as all cultures. The Lunes will work in great! Thank you for sharing.
Glad you can use them! I’d love to hear how it goes when the time comes.