Last year I invented a game called Digit Disguises and it has become a regular feature at One Hundred Factorial and other events. But before Digit Disguises came along, there was another game with a similar style of interaction that we played regularly, and this blog post is about that game. The game is called “Which Number Where?”

Which Number Where: A Game of Logical Deduction

Players:

• This game is designed for two players, or two teams.

Setting up:

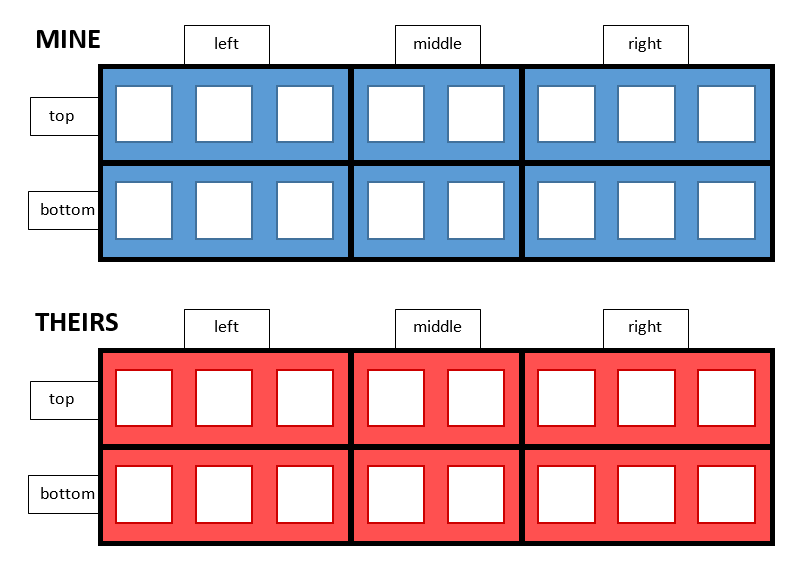
• Each player/team has two grids with six large boxes arranged in two rows, each containing little squares, one grid is labelled MINE and one is labelled THEIRS. See the picture below.
• Each player/team writes the numbers 1 to 8, each in a separate smaller square in the MINE grid, keeping the grid where the other player/team can’t see it. (I have a printable version with the rules on it that can be turned into battleships-style game stands here.)
• The six larger boxes are called “rooms”, and their location can be described by left, middle and right, and by top and bottom.

The goal:

• There are six rooms in the grid: top left, top middle, top right, bottom left, bottom middle, bottom right. You need to find out which room each of the other player’s eight numbers are in. It does not matter which box within the room each number is in, you just need to know which room each number is in.

Your turn:

• On your turn, ask any Yes or No question to the other player/team. You cannot ask any question other than one whose answer is Yes or No. Some examples are: “Is 1 in a top room?”, “Are there any empty rooms?”, “Are there any rooms with two even numbers?”
• The other player answers the question truthfully with either a Yes or a No.
• You can write notes to help you figure out what you know from the information you have so far.
• If the answer is YES, then you get another turn.
  If the answer is NO, then that is the end of your turn.

Ending the game

• On your turn, if you think you know where the other player’s numbers are, then ask one at a time if each number is in the location you think. If the answer is YES to all eight questions then you win! (If not, then at the first NO it’s the other player’s turn and the game continues.)

The story of Which Number Where

Once my wife and I were in a toy shop and we saw a game called “Guess Where?” by Milton Bradley for my family. It was pretty cute. Each player had a battleships-style fold-out stand with a picture of a house, which had slots in them to put little pictures of family members. The goal was to find out where the family members were in the house. For example, maybe Grandpa and the Cat were in the Kitchen. The thing that really intrigued me about the game was the fact that you were allowed to ask *any* yes or no question, and that a yes resulted in an extra turn.

I loved playing the game in our house, and so I wanted to buy a Guess Where set for the Maths Learning Centre, but when I tried, I discovered that the game was out of print. So instead in 2015 I designed a pen-and-paper version that I could print and play, or draw on a whiteboard and play. Of course to make it mathsy and easier to describe, I just used numbers instead of people, and so the game Which Number Where was born.

It’s been quite a staple at One Hundred Factorial over the years, and when I came to write this post, I was actually surprised at just how many years it had been since I made it! Here is a video from three years ago of a piece of a game in action so you can see how it works with real people:

Late night “Which Number Where” in the MLC pic.twitter.com/YcBdyWCR7x

— David Butler (@DavidKButlerUoA) October 4, 2017

And here is a game I played over Twitter two years ago so you can see all the questions that were asked in a game. Click on the twitter logo in the it and you will be taken to twitter where you can can scroll through the whole thread (no need to log into twitter to see it).

#whnwh game between @DavidKButlerUoA and @TobinSouth. You go first Tobin!

— David Butler (@DavidKButlerUoA) March 28, 2018

Thoughts on Which Number Where

I love Which Number Where! In many ways it’s quite similar to Battleships, but it is SO much cooler for two important reasons.

Firstly, you can ask any Yes-or-No question you like. This gives enormous freedom to the players, and people who play it really try to exploit this to get a lot of information all at once. Players also seem to like that they can be creative, and will tend to ask questions in a new or less obvious way even when a simple “Is 1 in the top left room?” would produce the same information.

Interestingly, using numbers allows for more freedom than the original Guess Where game. Numbers have a lot of features and properties that distinguish them, allowing for more creative ways to group them or refer to them. In games I have played, people have referred to even and odd numbers, prime numbers, powers of two, greater or less than a specific number, and several other properties. You can also use arithmetic on the numbers to help you get information. One of my personal favourite questions is of the form “Is the sum of the numbers in [insert collection of rooms] row even?”. This tells you how many odd or even numbers might be there, and if you’ve already located a few numbers, can actually give you rather a lot of information.

Secondly, the fact that you get another turn if you get a Yes answer forces people to think about how to ask their question. If you have a feeling about which answer is the most likely, you need to ask your question in such a way that that answer will produce a Yes rather than a No. And this makes you think about negating statements logically, which to me is really cool. My favourite is when someone asks something like “Is 8 outside the top left room?” as opposed to “Is 8 in the top left room?”

The two reasons above are inherent in the game itself, even just playing one-on-one. But the other thing that makes me love the game even more is when we play in teams. I adore listening to the discussion between the players in a team about what question to ask next, and about what information they have from the questions they have asked so far. It’s always fascinating to hear people’s thinking, and this game of pure logic is such an easy way to get that thinking on display.

I hope you enjoy playing (and listening to others playing) as much as I do.