Introduction
In an earlier post in this same series, I presented the following introduction, and I think it’s good enough to just repeat here…
The Cartesian plane is pretty cool. You think up an equation like y=x²+1 and find all the points (x,y) whose coordinates satisfy it, and you get a shape (in this case a parabola). Different kinds of shapes have different kinds of equations, and finding the places where shapes meet becomes solving equations simultaneously. Geometry becomes deeply connected to algebra and everything is lovely.
Then we create the complex numbers so that equations that weren’t previously solvable become solvable. Most notably the equation x²+1=0 gets the solutions x=i and x=-i. The simultaneous solutions to y=x²+1,y=0 are supposed to be the places where that parabola met the x-axis, only it doesn’t meet the x-axis. If the complex numbers are to be believed, that parabola meets the x-axis at the points (i,0) and (-i,0). But I can’t see those points in the original Cartesian plane! Maybe there is a way to add the new complex points to my existing Cartesian plane so that the graphs do look like they meet.
And there is a way. In 2016, I created such a way, and I have just made it better, producing a thing called an i-arrow. This is the full description, which I am shamelessly cutting-and-pasting into every post in this series. (Ooh look! This cutting-and-pasting is two layers deep!)
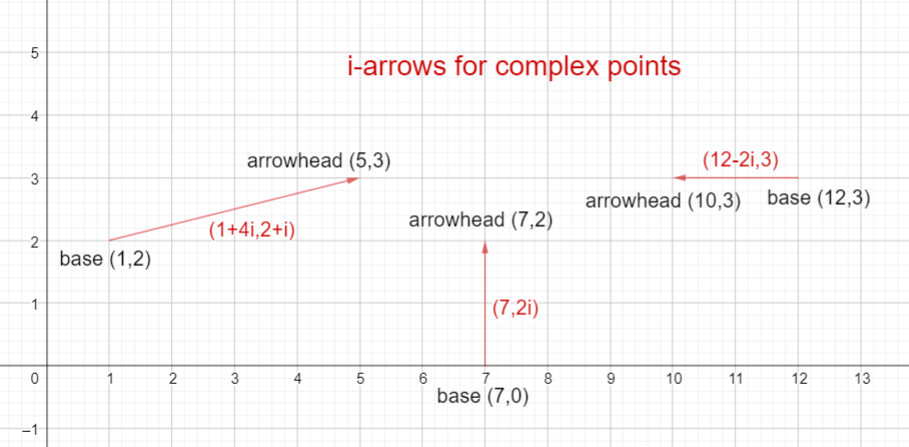
Every point with complex coordinates is represented as an arrow from one place to another on top of the Cartesian plane.
- Real points are dots on the Cartesian plane, the same as they have always been.
- The complex point (p+si,q+ti) is represented as an arrow (which I call an “i-arrow”), which is based at the point (p,q) and extends along the vector (s,t) to have its arrowhead at the point (p+s,q+t).
In the picture below, there are three examples of i-arrows.
- The complex point (1+4i,2+i) has been drawn as an i-arrow. Its base is at the point (1,2) and its arrowhead is at the point (1+4,2+1)=(5,2).
- The complex point (7,2i) has been drawn as an i-arrow. Its base is at the point (7,0) and its arrowhead is at the point (7,0+2)=(7,2).
- The complex point (12-2i,3) has been drawn as an i-arrow. Its base is at the point (12,3) and its arrowhead is at the point (12-2,3)=(10,3).
At this point in a previous post in this series, I reneged on my promise to illustrate where the parabola with equation y=x²+1 met the x-axis and instead talked about the complex points on a line. Now I will actually fulfill the promise. (Note I am not sorry that I didn’t do the parabola first. It was actually important to investigate the complex points on a line, because the x-axis itself is a line, so if I want to find out the complex points it shares with another object, I am going to need to know what complex points it has all on its own.)
Noticing things in the i-arrows on the graph of a quadratic function
When I first investigated complex points on parabolas, I wasn’t thinking of them as functions but as the sets of points that satisfy a condition. Only later did I consider them as functions. This time, I’ll go the other way around, and think of it as a function first. I’ll go one further, actually, and let my friend GeoGebra do some work for me to start with. GeoGebra is able to do complex number arithmetic, so I’ll sub in a selection of complex inputs, and draw the resulting (input,output) points as i-arrows and see what it looks like.
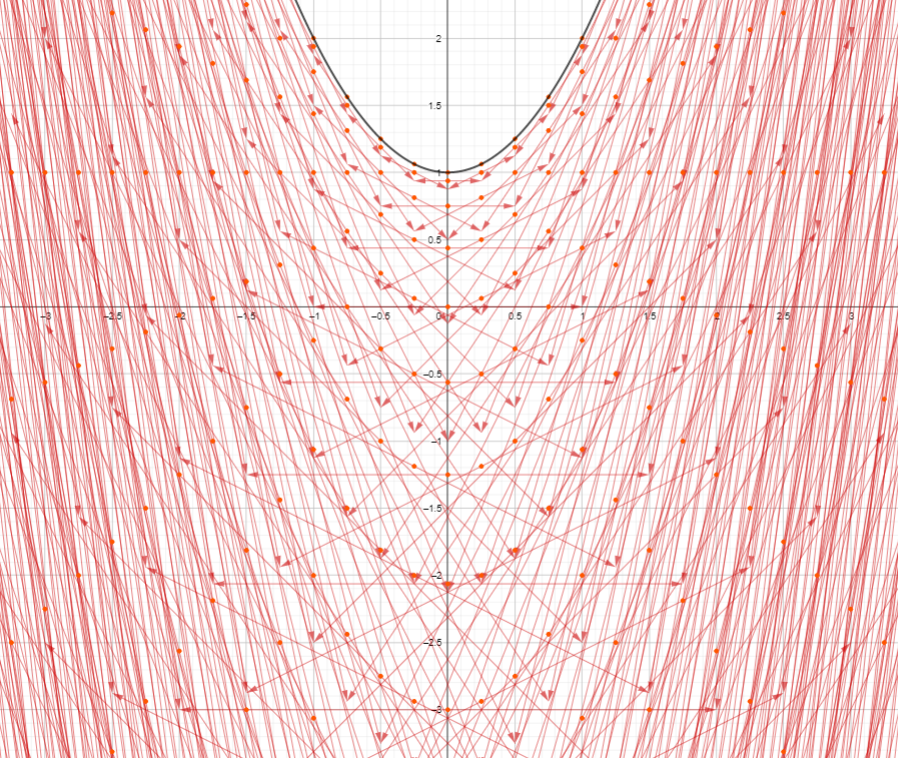
This is a view of the i-arrows that go with the complex points on the parabola that is the graph of the function f(x)=x²+1, made from substituting in x=p+si for both p and q ranging from to -5 to 5 in steps of 1/4. It doesn’t show the full length of every i-arrow, but a zoomed-in view so I can see the details I need to.
Have a close look at this picture and see what you can notice. Here are some things I notice:
- There are no i-arrows with base above the parabola, or with arrowhead above the parabola. In fact, the line segment that is each i-arrow is fully contained in the space below the parabola.
- Each base-point with an i-arrow has two i-arrows based there. I notice this most when looking at the base-points nearby to (0,0.75).
- Many of the points have two arrowheads there.
- There seem to be several upwards-opening parabolas made of base points, and several made of arrowheads too.
- I can also see several straight lines of base-points. Following those lines, they seem to be tangent to the parabola.
- There are collections of parallel i-arrows, and they get longer the further down they go. Also, their base-points are lined up vertically. I notice the set of horizontal i-arrows most, followed by a set nearby on either side.
- I can just see two horizontal i-arrows lying on the x-axis with their bases at the origin and arrowheads at (-1,0) and (1,0). That means they represent the complex points (0,-i) and (0,i), and since they line up with the x-axis, they are complex points on the x-axis. So these are where the parabola meets the x-axis, just as I expect.
There’s a lot to unpack there! I am extremely happy that this i-arrow representation afforded so many things to notice in one diagram. Such is the power of a good model, hey? Before I try to do the algebra that will explain the things I see, let me do another GeoGebra thing to investigate just one of these things more.
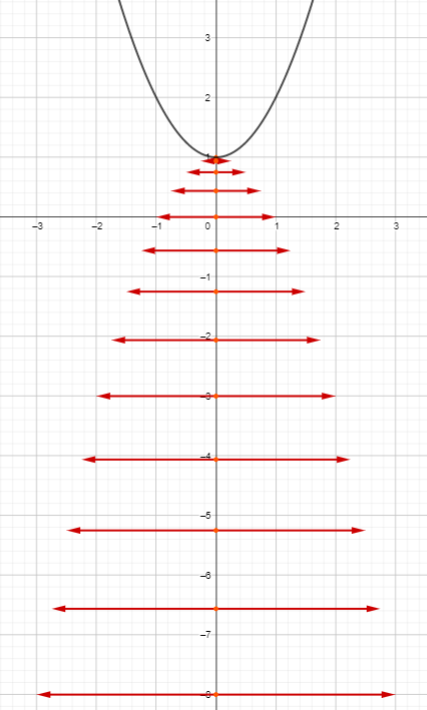
I noticed that those sets of parallel i-arrows had their base-points lined up vertically. All the i-arrows here are for complex points of the form (p+si,f(p+si)), with base point at (p,Real[f(p_si)]). A collection of base-points lining up vertically means that they belong to points with all the same value of p. That is, all the inputs have the same real part. And so what I did is I made GeoGebra draw the i-arrows for a selection of points made by inputting numbers with the same real part. Then I could look at just these ones. This tweet has the animated GIF that came out of that GeoGebra activity, but you can play with the original yourself here.
GIF showing complex points on the graph of f(x)=x^2+1. Each frame is the i-arrows for some (input,ouput) points where the inputs have the same real part.https://t.co/59TEdqxVrE
(WordPress is being weird about GIFs and this is the easiest way to deal with it) pic.twitter.com/00i0XdvnYK— David Butler (@DavidKButlerUoA) July 28, 2022
Have a look at that GIF (or play around with the GeoGebra tool) and see what you notice. Here are some things I notice:
- Every base point has two i-arrows, one in each direction.
- The i-arrows are shorter closer to the parabola and longer further away.
- The i-arrows for a specific real part are all parallel. In fact, it looks like they might be parallel with the tangent to the parabola at the matching point on the parabola.
- The arrowheads for the i-arrows for a specific real part look like they form a parabola of their own. This parabola is inverted relative to the original one, and the two appear to be tangent to each other.
- You can clearly see x-intercepts in the frame where the arrows are horizontal. The parabola of arrowheads looks like it is exactly the same as the real parabola, inverted and sharing the same vertex.
That’s a lot to notice, and my list of things to investigate is getting longer. I think it is this that is causing the collections of parallel lines in the original image, though, so that’s nice. Before I start on the algebra, I do want to do one more thing: I want to investigate what happens if I keep the imaginary part the same instead of the real part. Here’s the GeoGebra activity, and here’s the animated GIF.
GIF showing complex points on the graph of f(x)=x^2+1. Each frame is the i-arrows for some (input,ouput) points where the inputs have the same imaginary part.https://t.co/59TEdqxVrE
(WordPress is being weird about GIFs and this is the easiest way to deal with it) pic.twitter.com/EdLvnRZql3— David Butler (@DavidKButlerUoA) July 28, 2022
One last time, look to see what you notice. Here’s what I notice:
- The arrows momentarily disappear in the middle (which makes sense because that’s when the imaginary parts of the inputs are all zero).
- The base points in each frame follow a parabola, as do the arrowheads in each frame. These two parabolas look like they might be the same as the real parabola but shifted downwards.
- The three parabolas get further apart the further the imaginary part is from zero.
So those parabolas I saw in the first image seem to be caused by the outputs with all the same imaginary part. That’s good to have that mystery solved.
And now I have a long list of things that I want to confirm with some algebra.
Algebra (and some geometry)
Here goes! I’ll start by investigating the parabola as the graph of a quadratic function. I think some of the things I noticed above will need to use a different perspective, but for now I’ll stick with the function.
Let f(x) be a real quadratic function. That is, let f(x) = ax²+bx+c for real numbers a, b, c.
Consider the input x=p+si for real numbers p and s.
f(p+si)
= a(p+si)²+b(p+si)+c
= a(p²+2psi-s²)+b(p+si)+c
= ap²+2apsi-as²+bp+bsi+c
= ap²+bp+c-as²+2apsi+bsi
= ap²+bp+c-as²+(2ap+b)si
Looking at that equation, I can see ap²+bp+c, which is the value of f at p, and I can see 2ap+b, which is actually the value of the derivative of f at p! (This happened last time I investigated complex points on real parabolas and it’s just fascinating!)
So it looks like if f(x) = ax²+bx+c,
then f(p+si) = f(p) – as² + f'(p)si.
That looks like something I can work with!
The i-arrows based along a vertical line
Fix a specific value of p, and consider all inputs x=p+si with all possible values of s. It’s worth noting that i-arrows whose bases lie along a vertical line all must have come from such an input, since the real part of the x-coordinate of the matching complex point must all be the same.
I would like to show the following:
- The i-arrows produced this way are all parallel.
- The slope of the i-arrows produced this way are parallel to the tangent to the parabola at x=p.
- The arrowheads of the i-arrows produced this way form a parabola themselves. This parabola is inverted relative to the original and they are tangent to each other at the point where x=p.
- The i-arrows are horizontal when x=p passes through the axis of the original parabola, and when this happens, the parabola the arrowheads make is the same as the original, but inverted and sharing the same vertex.
Let’s see what I can do.
The complex point corresponding to the input p+si is (p+si,f(p)-as²+f'(p)si). Its i-arrow has base (p,f(p)-as²) and extends along the vector(s,f'(p)s), to finish at the arrowhead (p+s,f(p)-as²+f'(p)s).
The vector (s, f'(p)s) = s(1,f'(p)), which is parallel to (1,f'(p)). So the i-arrows are definitely all parallel since they’re parallel to this one vector. The slope of this vector is f'(p), which is indeed the slope of the tangent to the parabola at the point where x=p. Also note that the two i-arrows for opposite values of s are the same length and in opposite directions. Well, that was remarkably straightforward!
The arrowheads have coordinates (p+s,f(p)-as²+f'(p)s) for all values of s. For this to be a parabola, the y-coordinates must be a quadratic function of the x-coordinates.
Let x=p+s and y=f(p)-as²+f'(p)s.
Then x-p=s, so
y=f(p)-a(x-p)²+f'(p)(x-p)
= -a(x-p)²+f'(p)(x-p)+f(p).
This is a perfectly good quadratic function, and when I sub in x=p, the value comes out to f(p). Its leading coefficient is -a compared to the original leading coefficient of a, so it’s inverted relative to the original parabola. Finally, the derivative of this function is dy/dx = -2a(x-p)+f'(p), which does become f'(p) when x=p, so the two parabolas are indeed tangent at the point where x=p.
That just leaves what happens when the i-arrows are horizontal, which is supposed to happen when x=p passes through the vertex of the original parabola.
The i-arrows are parallel to (1,f'(p)), which is horizontal exactly when f'(p)=0. And f'(p)=0 exactly at the turning point of the parabola, where the tangent is horizontal. So yes the i-arrows are horizontal exactly when x=p passes through the turning point of the parabola.
When x=p does pass through the vertex, f'(p)=0 and so the equation of the parabola of arrowheads becomes
y= -a(x-p)²+0(x-p)+f(p)
= -a(x-p)²+f(p).
This is the equation of a parabola with vertex at (p,f(p)) and leading coefficient the exact opposite of the original. So yes it is the same parabola, inverted through the vertex
I wonder if all those other arrowhead parabolas are the same shape as the original too? Actually yes they have to be. All quadratic functions with leading coefficient a can be rewritten as y=a(x-c)²+h for some c and h, and are so the same shape as y=ax². All quadratic functions with leading coefficient -a can be rewritten as y=-a(x-c)²+h for some c and h, and are so the same shape as y=-ax², which is the same shape as y=ax² but inverted.
So everything I thought was true really is.
Aside: relationship to other representations
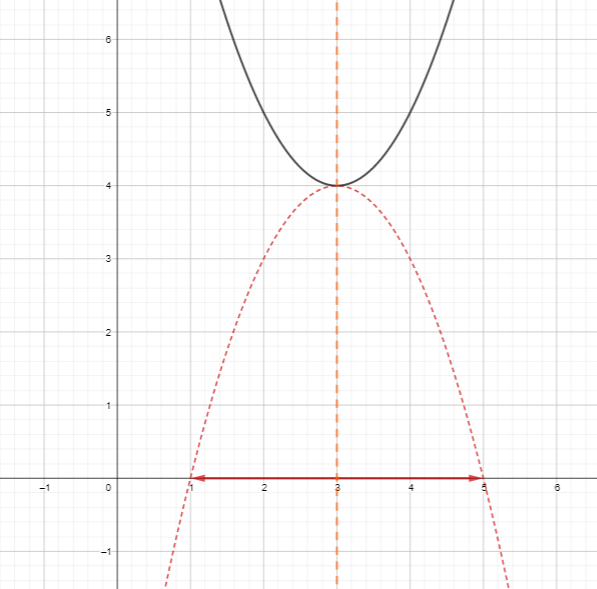
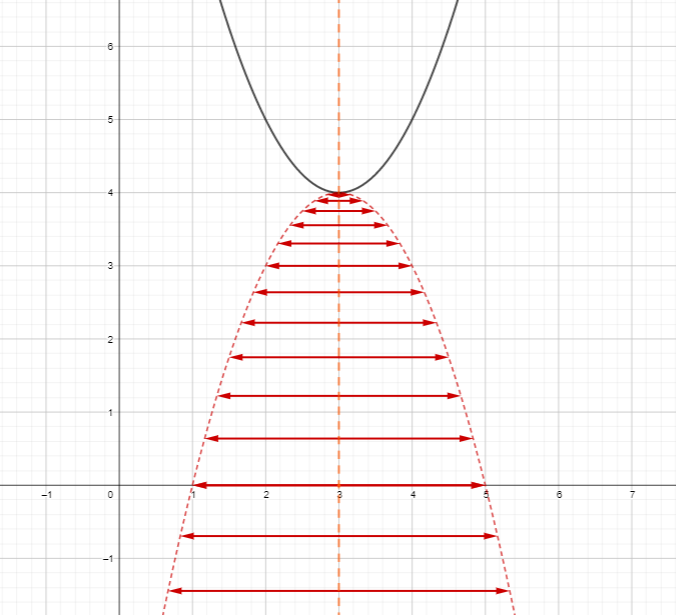
I will pause at this point to notice that you can abstract a graphical procedure for finding the complex roots of a quadratic function: invert the parabola at its vertex, then draw two equal-length i-arrows along the x-axis inside this new parabola from the axis of symmetry to the edge. The picture here shows the two complex roots of f(x)=x²+6x+13, which are 3-2i and 3+2i.
I have to say I do find such a diagram a bit unedifying. I much prefer to have all the i-arrows drawn in along that vertical line, to show that the curve itself is actually made of all the arrowheads of all those i-arrows.
The reason I drew the first picture is that I have seen it before in other people’s descriptions of how to visualise the complex solutions to real equations (though without the arrows on the picture). I’ve seen a pure description like the one I just gave (find where the inverted parabola meets the x-axis, x-coord of vertex is real part, distance from there to inverted parabola is imaginary part) just presented raw with only an algebraic explanation. But I’ve also seen a notable physical representation in Philip Lloyd’s phantom graphs. In those graphs, you imagine 3D graph with the complex plane as the x-y-axis and the real part of the output as the z-axis. Only the whole of this 3D graph is never drawn, just the curve of a parabola perpendicular to the original.
The thing I like most about my i-arrows is that the construction literally draws an actual representation of the actual complex points themselves, and also shows all the other complex points nearby, and indeed, you can draw all the complex points everywhere if you wanted to. As cool as Lloyd’s phantom graphs are, they are very phantom in the sense that they only exist in a 3D drawing outside the real plane. My i-arrows are drawn right there on the real plane itself. Also the Lloyd’s phantom graphs only represent a part of the actual complex point itself (the real part of the output) even if we did draw the whole 3D surface. My i-arrows show the complex part of the output too.
I’m sure I’m biased towards my own representation because it’s mine, but I don’t think I’m biased when I say it has a LOT of really cool features that make it useful beyond what phantom graphs are usually used for. I mean, the fact that you can find the complex points on a straight line by simply drawing an arrow on the line itself is just super amazing.
By the way, based on everything I know is true, I actually have a procedure for finding the complex points where the graph of a quadratic function meets any line it doesn’t meet in the real plane.
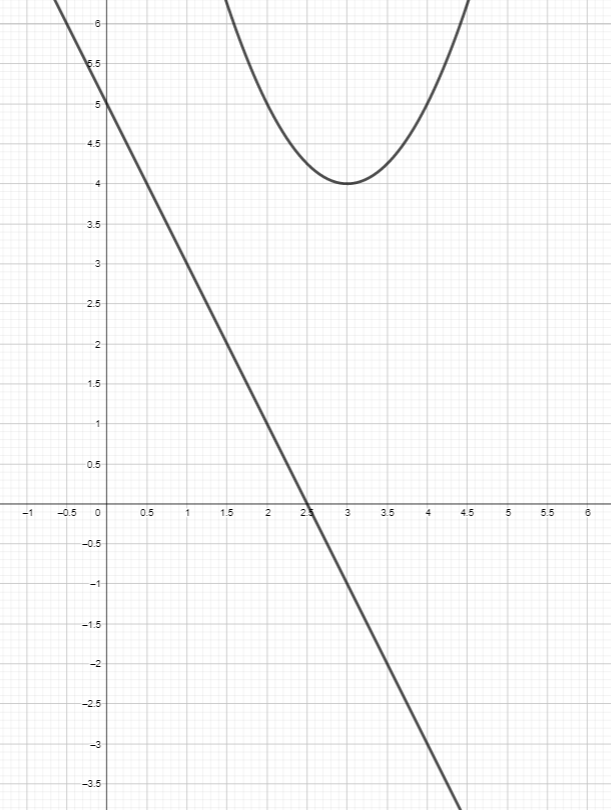
- Draw both the parabola and the line.
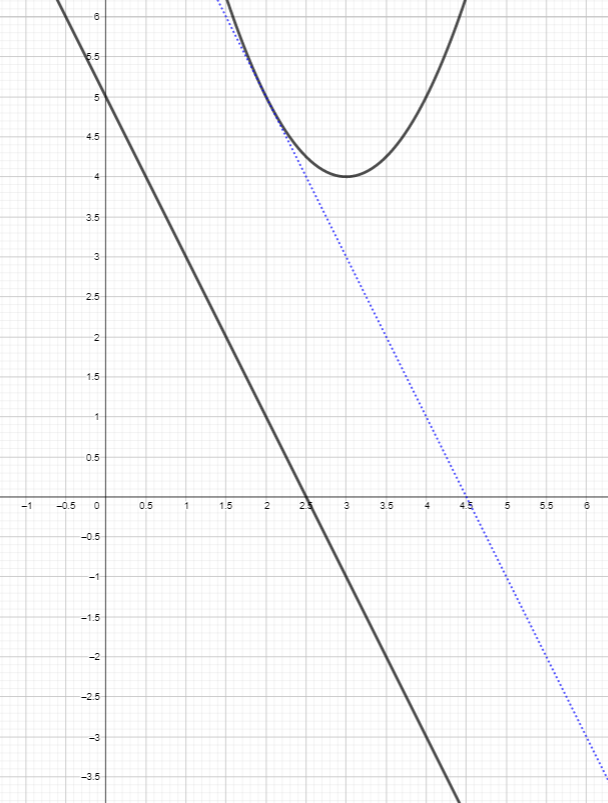
- Find the tangent to the parabola parallel to the line.
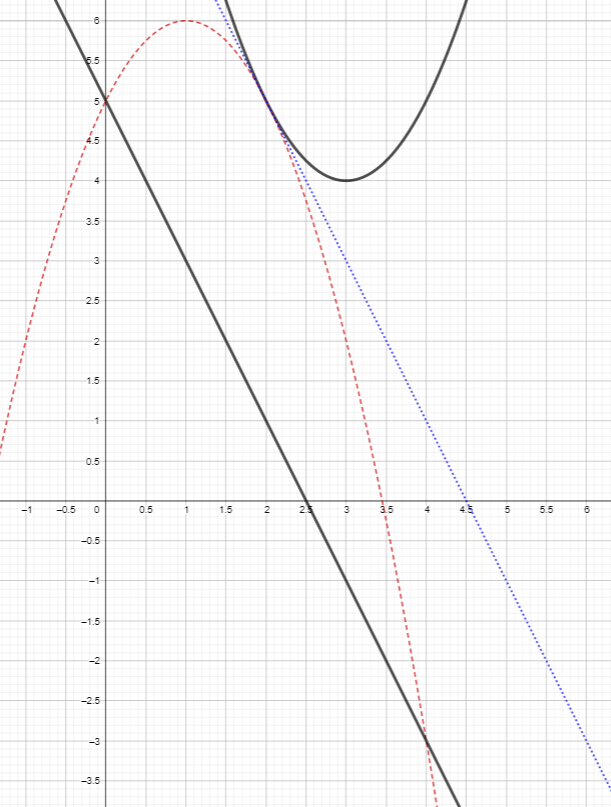
- Rotate the parabola 180° around the point where the tangent meets the parabola.
- Draw a vertical line from the parabola to the original line and find where it meets this line.
- Draw two i-arrows from this intersection point to the rotated parabola. These i-arrows are the complex points of the quadratic function on this line.
This collection of pictures illustrates this process for the function f(x)=x²+6x+13 and the line with equation y=5-2x. The intersection points are (2-2i,1+4i) and (2+2i,1+4i).
The i-arrows for inputs with the same imaginary part
Let me return to the quadratic function f(x) = ax²+bx+c for real numbers a, b, c, and the inputs x=p+si for real numbers p and s. As before, the complex point corresponding to the input p+si is (p+si,f(p)-as²+f'(p)si). Its i-arrow has base (p,f(p)-as²) and extends along the vector(s,f'(p)s), to finish at the arrowhead (p+s,f(p)-as²+f'(p)s). This time, let me fix s and vary p.
The set of base points are of the form (p,f(p)-as²). The function g(p)=f(p)-as² is still a quadratic function of p. Indeed, its graph is the same as that of y=f(x), just shifted downwards by as².
The set of arrowheads are of the form (p+s,f(p)-as²+f'(p)s). For this to be a parabola, just like last time, we need the y-coordinates to be a quadratic function of the x-coordinates. But this time, s is a constant.
Let x=p+s.
Then x-s=p.
And so y=f(x-s)-as²+f'(x-s)s.
The function f'(x-s) is linear, so subtracting it from the quadratic f(x-s) till makes a quadratic function like I noticed before. Let me do some more working…
y=f(x-s)-as²+f'(x-s)s
=a(x-s)²+b(x-s)+c-as²+(2a(x-s)+b)s
=a(x²-2sx+s²)+b(x-s)+c-as²+2as(x-s)+bs
=ax²-2asx+as²+bx-bs+c-as²+2asx-2as²+bs
=ax²+bx+c-2as²
=f(x)-2as²
Wow. It’s actually the exact same function as f(x), shifted down by 2as² — exactly twice as far as the parabola of base points. So cool. That’s all the observations that went with that GIF.
The i-arrows with a certain base or arrowhead
There were several observations right at the beginning about how many i-arrows were based at a certain point, and how many had their arrowhead at a certain point, and whether any part of an i-arrow passed through them. These are the last ones I want to think about.
Consider the function f(x)=ax²+bx+c for real a, b, c and suppose (p,q) is a point anywhere in the real plane. If there is an i-arrow in the graph of this function with base (p,q), then that means there are s and t such that the complex point (p+si,q+ti) satisfies the equation. So q+ti=f(p+si)=f(p)-as²+f'(p)si. Therefore
q=f(p)-as²,
t=f'(p)s.
In this scenario, p and q are fixed and we must find s and t.
From the first equation,
q=f(p)-as²
as²=f(p)-q
s²=(f(p)-q)/a
Depending on whether (f(p)-q)/a is positive, negative or zero, there will be two, one or zero solutions for s, and then once s is known the second equation from earlier will give one value of t. Therefore every point has either two, one or zero complex points of the parabola based there.
If a is positive, then (f(p)-q)/a is positive when f(p)-q>0, which is when q<f(p). The number q is the y-coordinate of the point in question, and f(p) is the y-coordinate of the point on the parabola with x-coordinate p. Since q<f(p), that means the point (p,q) is below the parabola! So every point below the parabola has exactly two i-arrows on the parabola’s graph based there.
If a is positive, then (f(p)-q)/a is negative when f(p)-q<0, which happens when the point (p,q) is above the parabola. In that case, there are no solutions for s, and so no i-arrows based there.
If a is negative, then the situation is reversed, and there are no i-arrows based at the points below the parabola, and two i-arrows based at the points above the parabola.
Regardless of whether a is positive or negative, (f(p)-q)/a can only be zero if q=f(p), which means (p,q) is a point actually on the real parabola itself. But also, the solution for s will be s=0, so the solution for t will be t=0, so there will actually be no i-arrow there but only the real point which we know is on the parabola already.
Putting all this together, whether a is positive or negative, this means that none of the points inside the curve of the parabola have i-arrows based there, and all of the points outside the curve of the parabola have exactly two i-arrows based there.
What about the arrowheads of the i-arrows?
If the point (g,h) is an arrowhead for some point on the parabola, then it is (p+s,f(p)-as²+f'(p)s) for some complex number p+si. This sets up two equations.
p+s=g
f(p)-as²+f'(p)s=h
I’ve seen something like this before, most recently when I was investigating i-arrows for inputs with the same imaginary part.
Write p=g-s and substitute into the second equation to get h=f(g-s)-as²+f'(g-s)s, which rearranges to h=f(g)-2as², based on my earlier experience.
So h=f(g)-2as²
2as²=f(g)-h
s²=(f(g)-h)/(2a)
And there are two, one or zero solutions for s, depending on whether (f(g)-h)/(2a) is positive, zero or negative. Just like last time, these happen when the point (g,h) outside the curve of the parabola, inside the curve, or on the parabola. Amazing. So glad I was able to reuse that algebra from before. Just to be clear, every point outside the curve of the parabola has two i-arrow arrowheads meeting there, and every point inside the curve has none.
Finally, every i-arrow is based at a point (p,q) outside the curve of the parabola (for example, below the curve if it opens upwards), and follows an arrow parallel to the tangent to the parabola at x=p. Since the whole real parabola is on the other side of the tangent from (p,q), the whole i-arrow must be on this side of the tangent and so miss the real parabola entirely.
Conclusion
So, I have confirmed pretty much everything I noticed before.
- Given a quadratic function, there are two of its i-arrows based at every point outside its curve, and two of its i-arrows with arrowhead at every point outside its curve.
- All of the i-arrows based at points along a vertical line are parallel to the tangent to the original parabola at the point where that line meets the parabola.
- Taking all the arrowheads for i-arrows based along a vertical line produces a parabola the same shape as the original, but rotated 180° around the point where the line meets the original parabola.
- You can find the unreal points where a line meets the parabola by first finding the tangent to the original parabola that is parallel to that line and using both of the two previous observations.
- In particular, the i-arrows based along the parabola’s axis of symmetry are all horizontal, and their arrowheads form a parabola the same shape as the original, but rotated around its vertex, and this allows you to find the complex x-intercepts of the original function.
All in all, I am very very happy. I really feel I understand a lot better where the complex points are on a parabola. But also I’m proud of both the algebra and geometry moves I made today, as well as how I structured this blog post around observation first and proof second.
There is only one promised blog post left in the series, which is about the unreal points on a circle, but it may take a while to finish, since I come out of quarantine tomorrow.
These are all the other posts in this blog series, if you want to find them easily:
- Where the complex points are: i-arrows
- The complex points on a line using i-arrows
- Further updates on the complex points on an unreal line using i-arrows
- The complex points on a line in finite geometry using i-arrows
- The complex points on a parabola using i-arrows (YOU ARE HERE)
- The complex points on real circles using i-arrows
- The complex points on unreal circles using i-arrows
- The line joining two complex points using i-arrows