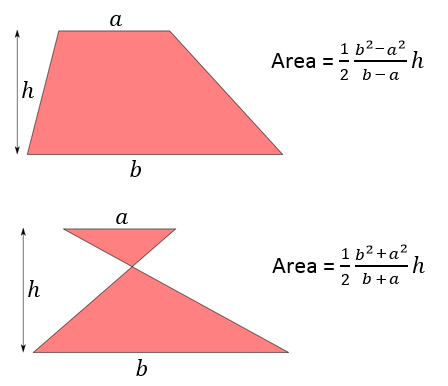
Recently I started thinking about the properties of the following shape, which I like to call the “Crossed Trapezium”. It has two parallel edges, which are joined by two crossing lines.
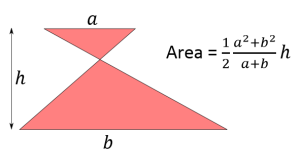
Because of Quarter the Cross, I’ve also been interested in areas recently, so of course I had a desire to know more about the area of the crossed trapezium. (If you haven’t heard of Quarter the Cross, then you will soon, I promise.) Surely there should be some sort of simple formula to calculate the area, I thought. Well there is, and it’s this:
Here’s how I figured it out (a PDF version of this is here):
(I was particularly proud of using the fact about the ratio of the areas of similar shapes being the ratio of the squares of one of their edges.)
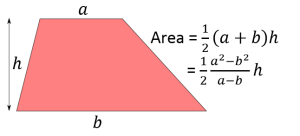
I was rather surprised by the result, though. The a+b on the bottom had no hope of cancelling out with the a2+b2 on the top, and so it seemed very complicated. Also it didn’t seem to have much of a relationship with the formula for the area of an ordinary trapezium.
But then I noticed this:
So it turns out that the formulas for the areas of the two kinds of trapezium are in fact very similar! It occurred to me that there must be a good reason why there is a + in one formula and a – in the other, and I fiddled around with it for some weeks until I came up with this working (this is also in that same PDF document):
So there you have it: the crossed trapezium is the union of two similar triangles and the ordinary trapezium is the difference of two similar triangles, which is why their areas are given by these formulas:



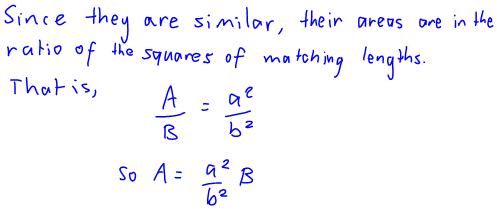
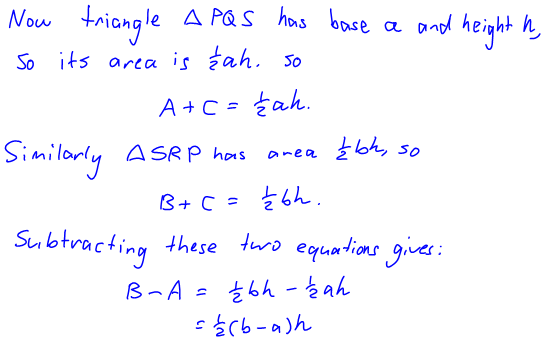

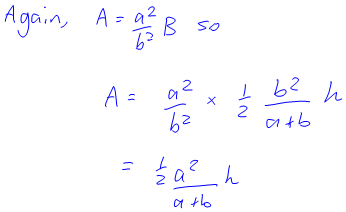
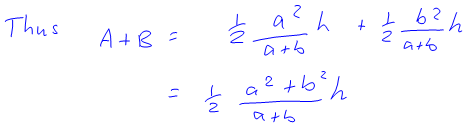

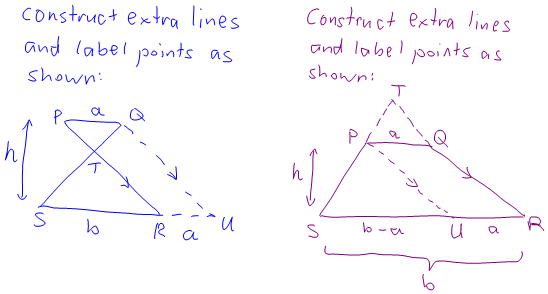




Related factoid: in the figure you dub a “crossed trapezium”, the two triangles that were removed from the original trapezium have equal area.
Also, this useful figure pops up in a lot of ratio problems we tweet about, such as “method 4” solution in this octagon problem:
https://casmusings.wordpress.com/2014/11/13/squares-and-octagons-a-compilation/
Interestingly, not only are they equal area, but their areas together are hab/(a+b). Most interesting.
The relationship between the formulas for the ordinary and crossed trapezia is rather elegant. Unfortunately, the formula for the ordinary trapezium isn’t numerically well-behaved: if the two bases are the same length, then the a-b term is zero, and the result is undefined; if the two bases are nearly the same length, a-b is very small, and calculations on a computer may be inaccurate.
An alternative formula without that problem is:
a = 1/2 * ((b^2 + a^2 + 2ab) / (b + a)) * h
Which is still similar to the formula for the crossed trapezium, but doesn’t have an obvious (to me) geometric interpretation! Something about the triangles cut out of the sides?
Thanks for sharing this interesting work. I first started thinking of areas for crossed trapezia whilst preparing lessons on motion in a straight line for my students. I have been looking at the vel-time graph for a period of constant acceleration where the sign of the velocity changes. The area trapped between the graph and the t-axis is a crossed trapezium. Interestingly, if you consider the area in the first triangle to be postive and the second to be negative (consistent with calculating displacements), the formula for the area of the trapezium is unchanged from the canonical one.