Why I’m doing this
I foolishly said this on Twitter about a month ago:
@DavidKButlerUoA @MathguyArt on the line at infinity? Tell me about those!
— Tina Cardone (@crstn85) June 14, 2016
At the time I declared this was a bit of a can of worms and I promised to write something and post it later. Well, here it is. But it might take a few blog posts to untangle it. In this post, I’m going to talk about how we can construct the line at infinity.
What do parallel lines have in common?
Let’s think about the geometry of the flat plane, and focus on just the straight lines and the points. Forget about the circles and the conics and the functions, just look at the straight lines. (I’m not even going to use the word straight any more, since straight lines are the only kinds of lines we’re going to look at.)
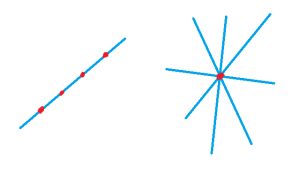
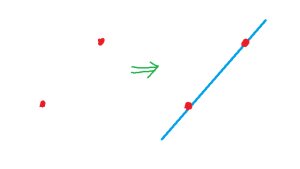
What can you say about points and lines? Well, if I had a single line, I could certainly locate a lot of points on the line. And if I started with a single point, there would be a lot of lines through that point.
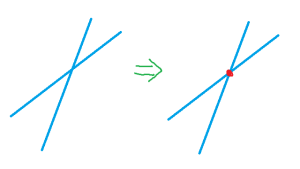
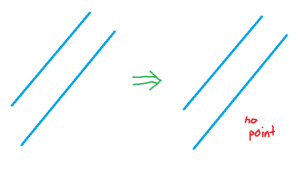
If I had two points, then there would be exactly one line that I could draw through both of those points. And if I had two lines, then … well that’s not so easy. Either the two lines meet and there would be exactly one point they share, or they don’t meet at all, and we’d call them parallel.
But it’s not as if parallel lines have nothing in common. If you draw two lines parallel to each other, then they are obviously very very similar. Some might say they are the most similar kinds of lines. I find that rather interesting: somehow, by not meeting, two parallel lines are inextricably linked. What is it that they have in common?
Well, one thing they have in common is their slope. Two parallel lines have the same slope. If we’re thinking algebraically, you can rearrange their equations so that they have equations like y=mx+c and y=mx+d, for the same m but different c and d. Of course if they’re vertical, then the equations can’t be rearranged to look like this, but we can still say they have the same “slope” of “no slope”.
So, even if parallel lines don’t share a point, they do share a slope. Interestingly, any two lines which do share a point, don’t share a slope. So it seems that two lines must share one thing: either they share a point or a slope.
A new kind of point
Now that we have this idea that two lines must share something, they are a lot more like points.
Two points share a unique line; two lines share a unique point-or-slope.
This has a kind of pleasant symmetry about it. It would have even more symmetry if it was
Two points-or-slopes share a unique line; two lines share a unique point-or-slope.
Only it is this! If I pick a point and a slope, there is a unique line through that point with that slope! (You may say that two slopes don’t share a line, and yes I realise this, but I’ll get back to it I promise.)
So it seems that slopes and points are the same kinds of thing, at least with respect to how they interact with lines. I think this is rather cool. It’s a bit philosophical, but often cool things are. The really nice bit of philosophy is this: if points and slopes are so similar, why don’t I declare that a slope is a new kind of point? Then I can just say
Two points share a unique line; two lines share a unique point.
Can I just do that? Can I call something by a new name? It’s not as if the slopes really are points — I can’t see them or point to them (excuse the pun). But that sort of thing has never stopped us mathematicians before (think of the number 0). Plus, perhaps there is a way to see them after all…
Seeing infinity
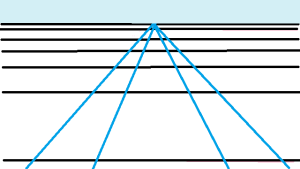
If you look at a pair of parallel lines from above, then it actually does look like they ought to meet somewhere. Look out to the horizon and there they seem to meet. Of course if you walk towards it, that intersection point just keeps getting further away. However far you go towards it, it’s still just as far away. Of course, that’s because the point isn’t really there, it just looks like it is. But it does look like it’s there, and you feel like if only you went far enough, you’d see it.
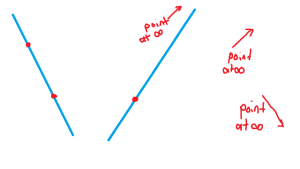
This is the extra bit of philosophy we need to legitimise calling our slopes points. It feels like two parallel lines actually do meet, but they meet infinitely far away. Philosophically, we know the two parallel lines do share something that acts like a point acts — it’s their slope. So what we do is we declare that our slope-points we made earlier are called “points at infinity”.
It’s not just matching with our visual instincts either. If you were going to add a new point to a line, it would have to go somewhere, but there’s no space over here to put that extra point — our lines are already full. We’re going to have to add our extra point at the end of our line — that is, out there at infinity.
So now we have two kinds of points: we have our original common-or-garden points that we can see. And we have our new points at infinity that we can’t see. These points at infinity aren’t really there in the world, but they are really there in our minds — they are the slopes of the lines, and we know for sure that two parallel lines do indeed share a slope. We know that slopes are like points in the way they interact with lines, and so it’s ok to call them points. But we can’t see slopes either, so in a way it is only fitting to call them “points we can’t see”.
We can now start filling out our new terminology with some imagination. Say I have a point and I want to draw a line through it of a certain slope. Well, that slope is a “point at infinity”, so drawing the line we want would be joining this point to the appropriate “point at infinity”. I imagine it as standing at this point and looking out to infinity in the direction I want the line to go, and drawing the line in that direction. I am still joining it to that point at infinity, I just won’t ever get there.
You might be thinking that surely I could have looked in the opposite direction and drawn my line that way. Well, yes I could. And that’s where the analogy needs a bit of tweaking. Remember that these points at infinity are not really points that live in a real place: they are slopes that don’t live anywhere but in our minds. It looks like if we want them to live in the real world, we’re going to need them to be both in front of us and behind us. Needs must.
The line at infinity
So there’s only one thing left to do: we have to deal with the niggling little detail that two points don’t quite share a unique line. We know that two ordinary points share a unique line (that was true before), and we know that an ordinary point and a point at infinity define a unique line (that’s an ordinary point and a slope, really).
But what about two points at infinity? That’s two slopes, and we know there’s no lines with two slopes. Well that’s ok, we’ll just collect all the slopes together to make one new line. Since this line is made up entirely of points at infinity, we’ll call it the line at infinity.
From now on, we will start talking about the points at infinity as if they were really real points, that really were really at infinity. If we try hard we can remember that they’re really just slopes, but we don’t have to do that to make the maths work. Our imagination will tie in fine with how the maths works, because we’ve carefully made it do so. We’ve had to bend our imagination a little to make the concept of a really real line at infinity fit with our words and pictures, but that’s ok, we can always check back with the slopes if we need to make sure. Plus, really cool maths often requires a change of perspective.
(The next post in the series is all about coordinates, and the one after that is about conics.)

[…] came to do that, I realised it’s a can of worms that will take a few blog posts to untangle. Last time, I talked about how I construct and think about the line at infinity […]
[…] I talked about what the line at infinity is. We noticed that a set of parallel lines all share a slope, so we elevated all the slopes to the […]