This blog post is about a metaphor I use when I think about the order of operations: the idea that the various operations are stickier than the others, holding the numbers around them together more or less strongly.
The idea begins with the fundamental idea in arithmetic, that maths working proceeds by replacing something with something else you know it’s equal to. When working on an expression involving numbers and operations, to proceed further, you need to find a piece of the expression you can replace. The order of operations describes the rules for when you are allowed to replace right now a part of an expression involving numbers and an operation. (I usually draw the order of operations using the Operation Tower.)
For example, look at the following expression:
6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
There are several pieces of this you can replace with their result safely without breaking the rules of the order of operations. You can replace the 6 ÷ 3 with 2, or the 7 – 2 with 5, or the 2³ with 8, or the 8+2 with 10.
6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
= 2 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
= 6 ÷ 3+ 5 – 5 + 8 × 2³ + 6 × (8+2)
6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
= 6 ÷ 3 + 7 – 2 – 5 + 8 × 8 + 6 × (8+2)
6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × (8+2)
= 6 ÷ 3 + 7 – 2 – 5 + 8 × 2³ + 6 × 10
When people describe the order of operations, we usually talk about it saying which operations can be done first, saying that some operations should be done earlier than others, and you do them left to right if there’s no preference, and brackets override the order. That’s how I usually describe it.
But this doesn’t quite match with what I describe above. For a start, it’s actually correct to do the subtraction before the power even though the division is supposed to be done earlier than subtraction. I usually tell students that the order of operations just tells you which operations go before others when they’re nearby to each other. So that subtraction is too far away from the power to really make a difference if I do it first or second.
But then there’s weird problem with subtractions near to additions and each other. I can’t replace the 2 – 5 in the above expression because that would stuff up the 7 – 2. But there is nothing in my description of “nearby” that would tell you there is this preference. You have to fall back on the “left to right” idea from the traditional order of operations again.
For some reason I really don’t like this. The left-to-right idea seems completely against all the effort we take to teach students to be flexible with their arithmetic, where we encourage them to pull numbers apart and put them together in new ways to make the arithmetic easier to do and to understand. Plus it’s not how I actually do it. When I read an expression, I scan across the whole thing first, and then I pick a spot to work on that feels right to me, deciding that it’s ok to work on that bit because it doesn’t cause problems with the things around it. I make my decision of which operation to do locally, not globally.
And there is one final thing: when we port all of this order of operations stuff up to algebra, we start to think about terms, which are pieces of expressions joined together with multiplication and exponents. We learn to see those things as one blob, separated by the minus and plus signs.
So I reckon that the order of operations in my head is actually not about which operation should be done first, but which operations do a better job of sticking numbers together.
In the above expression, the smaller expression 6 ÷ 3 is stuck together more strongly than the expression 3 + 7. It’s safe to pull out the 6 ÷ 3 and replace it with a 2, but not safe to pull out the 3+7. So ÷ is stickier than +. I imagine pulling at the 3+7 to try to replace it with a 10, but the 3 breaks off when I do that because the “6 ÷” is stuck more strongly than the + 7.
Also, in the above expression, I notice that I think it’s safe to pull out the 7 – 2 to replace it, but it’s not safe to pull out the 2 – 5. It must be that – is stickier on its right-hand side than it is on its left-hand side. If I see a ” – 2 -” then I know the whatever number is before the 2 is stuck more strongly to the 2 than whatever number is after the 2.
So it seems that the operations have different levels of stickiness, and the ones that aren’t commutative stick stronger to one side than the other.
But there is one thing left to think about: grouping symbols like brackets and the horizontal bar. They’re not operations, but they do play a part in holding expressions together. Indeed, for brackets holding things together is their entire purpose. In fact, the stuff between the brackets, or under the bar in a square root, all that stuff is wrapped up together into one number and can be treated as one number for the purposes of moving stuff around in algebra. So maybe the grouping symbols work more like a box you put things into, with operations outside stuck to the box itself rather than to the stuff inside it.
This box idea is actually quite useful, because it helps me to sort out problems with how I think about the distributive law. A lot of students will see something like 3(x+2)² and try to do (3x+6)² . What they did there was replace 3(x+2) with 3x+6. But the brackets are holding the x+2 in a box, so that it might as well be 3B². In that case, the exponent sticks to the box much more strongly than the 3, so you can’t pull out the 3B to replace it with something else, though you can pull out the B² to replace it with something else.
So those are my fairly rambling thoughts that explain why I rather like this way of describing the order of operations. I’ve used the stickiness metaphor before, but not until now have I thought about it as deeply as this, and I actually like it even more than I used to, now that I’ve connected it to replacing.
So, to sum up, here’s how I think about the metaphor:
- To do maths working, you pull out an expression to replace it with something it’s equal to.
- Operations are glue that stick numbers together, preventing you from pulling them out if they’re stuck too well.
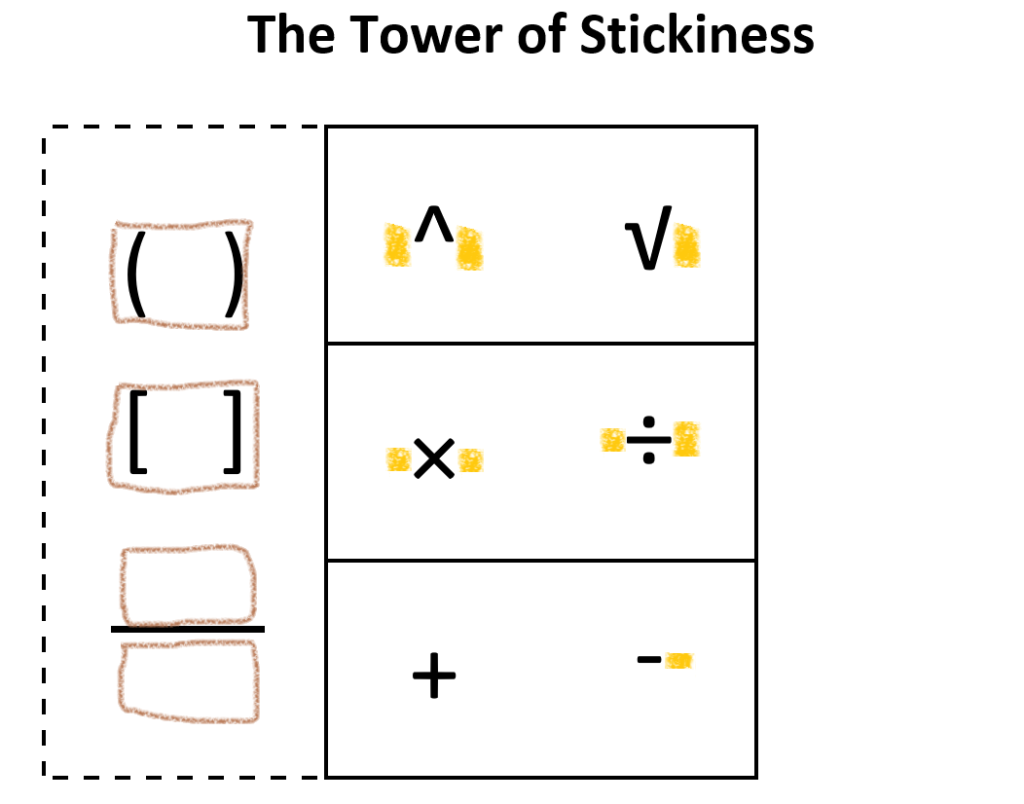
- Some operations are stickier than others: × and ÷ are stickier than + and -; ^ and √ are sticker than × and ÷.
- Some operations are stickier on one side than the other: – and ÷ are stickier on their right-hand side.
- If you see …number[operation]number…, you can only pull that expression out to replace it if the operations on the other sides of the numbers equal or less sticky than the one between.
- Grouping symbols are boxes that hold expressions inside them.
- You can always replace the stuff inside a box without affecting the stuff outside the box.
And so in my head, the Operations Tower has become a Tower of Stickiness:
PS: I had this thought that I need to add here, lest I forget it. I reckon that it would be much easier to help people understand the idea of an order of operations that allows for flexibility if you did just addition and subtraction first, without any other operations. Knowing that 7+5 – 3 – 2 has a few choices for how it can be done would be a great advantage before you introduce multiplication and division into the mix. Plus, a string of additions and subtractions could easily represent a story of adding and taking and so your learners would know what the correct answer is supposed to be! Anyway, that’s a thought to wrestle with another day.



